符号执行技术笔记

此前没有接触过符号执行，所以本文是在我学习过程中对一些好的文章的摘录，算是方便我日后回顾学习，特别感谢r1ce和K0rz3n的文章，所有参考连接将放在文末。如果我后续研究到符号执行技术相关的内容大概会补充进来。文末有一些我读文章时候的疑问，读完本文再看，可能有助于你的理解。

0x1 通俗地解释符号执行

Wiki中的定义是：在计算机科学中，符号执行技术指的是通过程序分析的方法，确定哪些输入向量会对应导致程序的执行结果为某个向量的方法(绕)。通俗的说，如果把一个程序比作DOTA英雄，英雄的最终属性值为程序的输出（包括攻击力、防御力、血槽、蓝槽），英雄的武器出装为程序的输入（出A杖还是BKB）。那么符号执行技术的任务就是，给定了一个英雄的最终属性值，分析出该英雄可以通过哪些出装方式达到这种最终属性值效果。

可以发现，符号执行技术是一种白盒的静态分析技术。即分析程序可能的输入需要能够获取到目标源代码的支持。同时，它是静态的，因为并没有实际的执行程序本身，而是分析程序的执行路径。如果把上述英雄的最终属性值替换成程序形成的bug状态，比如，存在数组越界复制的状态，那么，我们就能够利用此技术挖掘漏洞的输入向量了。

可以发现，符号执行技术是一种白盒的静态分析技术。即，分析程序可能的输入需要能够获取到目标源代码的支持。同时，它是静态的，因为并没有实际的执行程序本身，而是分析程序的执行路径。如果把上述英雄的最终属性值替换成程序形成的bug状态，比如，存在数组越界复制的状态，那么，我们就能够利用此技术挖掘漏洞的输入向量了。

这里再举一个简单的例子，让大家有深刻的理解。

以下面的源代码为例子：

int m=M, n=N, q=Q; 
int x1=0,x2=0,x3=0;
if(m!=0)
{
    x1=-2;
}
if(n<12)
{
    if(!m && q)
    {
        x2=1;
    }
    x3=2;
}
assert(x1+x2+x3!=3) // if =3 then program crash

上述代码是一个简单的c语言分支结构代码，它的输入是M,N,Q三个变量；输出是x1,x2,x3的三个变量的和。我们这里设置的条件是想看看什么样的输入向量<M,N,Q>的情况下，得到的三个输出变量的和等于3.

那么我们通过下面的树形结构来看看所有的情况：

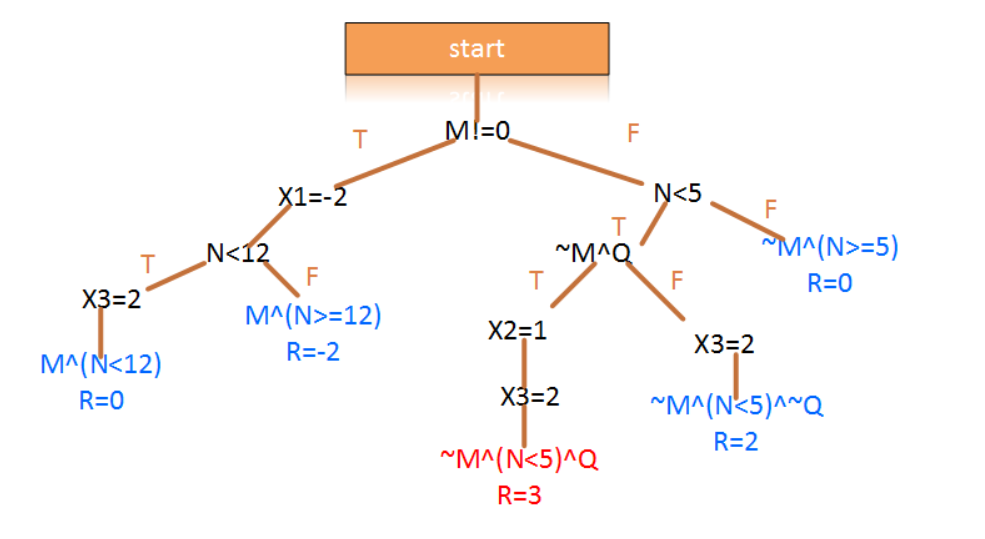
上面的分析图把所有可能的情况都列举出来了，其中，叶子节点显示的数值表示当前输入情况下，可以得到的数值。（比如，如果英雄出装是M^(N<12)，那么最终的属性值R=0）。其中M^(N<12)表达的是，M是非零值且N要小于12，Q为任意值的情况下，得到R=0。可以发现，当条件为~M^(N<5)^Q时，得到了最终结果等于3.即，我们通过这种方式逆向发现了输入向量。如果把结果条件更改为漏洞条件，理论上也是能够进行漏洞挖掘了。

对于如何根据最终得到的结果求解输入向量，已经有很多现成的数学工具可以使用。上述问题其实可以规约成约束规划的求解问题（更详细的介绍看这里：Constraint_programming ）。比较著名的工具比如SMT（Satisfiability Modulo Theory，可满足性模理论）和SAT。

但是在实际的漏洞分析过程中，目标程序可能更加复杂，没有我们上面的例子这么简单。实际的程序中，可能包含了与外设交互的系统函数，而这些系统函数的输入输出并不会直接赋值到符号中，从而阻断了此类问题的求解。

比如下面的这个包含了文件读写的例子：

int main(int argc, char* argv[])
{
    FILE *fop = fopen("test.txt");
    ...
    if(argc > 3)
    {
        fputs("Too many parameters, exit.", fop);
    }
    else
    {
        fputs("Ok, we will run normally.", fop);
    }
    ...
    output = fgets(..., fop);
    assert(!strcmp(output, "Ok, we will run normally.")); // if str is "OK,..." then program crash
    return 0;
}

上述示例代码中，想要发现什么情况下会得到输出”Ok, we will run normally.”这个字符串。通过一系列的执行到if语句，此时，根据程序输入的参数个数将会产生两个分支。分支语句中将执行系统的文件写操作。**在传统的符号执行过程中，此类函数如果继续沿着系统函数的调用传递下去的话，符号数值的传递将会丢失。**而在之后的output = fgets(…, fop);这行代码中，符号从外部获得的数值也将无法正常的赋值到output中。因此，符号执行无法求解上述问题，因为在调用系统函数与外设交互的时候，符号数值的赋值过程被截断了。

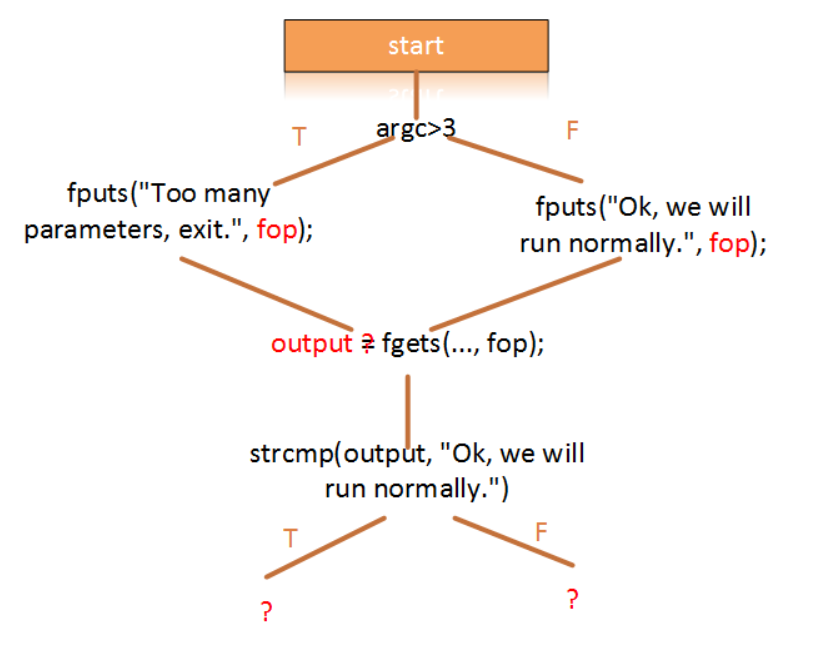
为了解决这个问题，最经典的项目就是基于LLVM的KLEE（klee)它把一系列的与外设有关的系统函数给重新写了一下，使得符号数值的传递能够继续下去。从比较简化的角度来说，就是把上面的fputs函数修改成，字符串赋值到某个变量中，比如可以是上面的fop里面。再把fgets函数修改成从某个变量获取内容，比如可以是把fop的地址给output。这样，就能够把符号数值的传递给续上。当然，这里举的例子是比较简单的例子，实际在重写函数的时候，会要处理更复杂的情况。在KLEE中，它重新对40个系统调用进行了建模，比如open, read, write, stat, lseek, ftruncate, ioctl。感兴趣的读者可以进一步阅读他们发表在OSDI2008年的论文（KLEE-OSDI08)他们的文章深入浅出，非常适合学习。

0x2 从公式原理上理解符号执行

符号执行的关键思想就是，把输入变为符号值，那么程序计算的输出值就是一个符号输入值的函数。这个符号化的过程在上一篇AEG文章中已有简要阐述，简而言之，就是一个程序执行的路径通常是true和false条件的序列，这些条件是在分支语句处产生的。在序列的第i位置如果值是true，那么意味着第i个条件语句走的是then这个分支；反之如果是false就意味着程序执行走的是else分支。

那么，如何形式化地表示符号执行的过程呢？程序的所有执行路径可以表示为树，叫做执行树。接下来我们就以一个例子来阐述通过符号执行遍历程序执行树的过程。

int twice(int v){
	return 2*v;
}

void testme(int x, int y){
	z = twice(y); 
	if(z == x){
		if(x > y+10)
			ERROR;
		}
	}
}

/* simple driver exercising testme() with sym inputs */
int main(){
    x = sym_input();
    y = sym_input();
    testme(x, y);
    return 0;
}

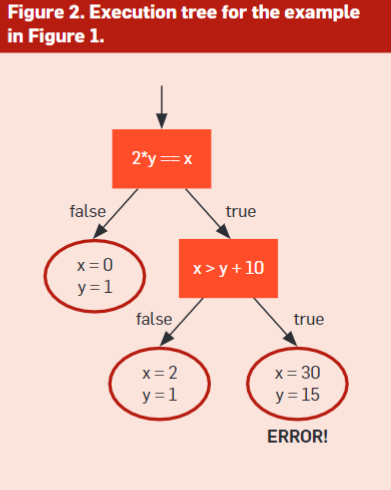
代码中，testme()函数有3条执行路径，组成了上图中的执行树。直观上来看，我们只要给出三组输入就可以遍历这三个路径，即图中圆圈中的x和y取值。符号执行的目标就是能够生成这样的输入集合，在给定的时间内探索所有的路径。

为了形式化地完成这个任务，符号执行会在全局维护两个变量。其一是符号状态 $\sigma$ ，它表示的是一个从变量到符号表达式的映射。其二是符号化路径约束PC（或者叫路径条件），这是一个==无量词的一阶公式==，用来表示路径条件。在符号执行的开始，符号状态 $\sigma$ 会先初始化为一个空的映射，而符号化路径约束PC初始化为true。 $\sigma$ 和PC在符号执行的过程中会不断更新。在符号执行结束时，PC就会用约束求解器进行求解，以生成实际的输入值。这个实际的输入值如果用程序执行，就会走符号执行过程中探索的那条路径，即此时PC的公式所表示的路径。

我们以上图的例子来阐述这个过程。当符号执行开始时，符号状态 $\sigma$ 为空，符号路径约束PC为true。当我们遇到一个读语句，形式为var=sym_input()，即接收程序输入，符号执行就会在符号状态 $\sigma$ 中加入一个映射 $var \rightarrow s$ ，这里s就是一个新的未约束的符号值。上述代码中，main()函数的前两行会得到结果 $\sigma=\lbrace x \rightarrow x_0, y \rightarrow y_0\rbrace$ ，其中 $x_0$ 和 $y_0$ 是两个初始的未约束的符号化值。

当我们遇到一个赋值语句，形式为v=e，符号执行就会将符号状态 $\sigma$ 更新，加入一个v到 $\sigma(e)$ 的映射，其中 $\sigma(e)$ 就是在当前符号化状态计算e得到的表达式。例如，在代码执行完第6行时， $\sigma=\lbrace x \rightarrow x_0, y \rightarrow y_0, z \rightarrow 2y_0\rbrace$ 。

当我们遇到条件语句if(e) S1 else S2，PC会有两个不同更新。首先是PC更新为 $PC \wedge \sigma(e)$ ，这就表示then 分支；然后是建立一个新的路径约束PC’，初始化为 $PC \wedge \neg \sigma(e)$ ，这就表示else分支。如果PC是可满足的，即可以给符号分配一些实际值，那么程序执行就会走then 分支，此时的状态为：符号状态 $\sigma$ 和符号路径约束PC。同样，如果PC’是可满足的，那么会建立另一个符号执行实例，其符号状态为 $\sigma$ ，符号路径约束为PC’，走else分支（请注意，与具体执行不同，符号执行技术可以同时使用两个分支，从而产生两个执行路径）。如果PC和PC’都不能满足，那么执行就会在对应路径终止。例如，第7行建立了两个不同的符号执行实例，路径约束分别是 $x_0=2y_0$ 和 $x_0 \not= 2y_0$ 。在第8行，又建立了两个符号执行实例，路径约束分别是 $(x_0=2y_0) \wedge (x_0 > y_0 + 10)$ 和 $(x_0=2y_0) \wedge (x_0 \leq y_0 + 10)$ .

如果符号执行遇到了exit语句或者错误（指的是程序崩溃、违反断言等），符号执行的当前实例会终止，利用约束求解器对当前符号路径约束赋一个可满足的值，而可满足的赋值就构成了测试输入：如果程序执行这些实际输入值，就会在同样的路径结束。例如，在上图例子中，经过符号执行的计算会得到三个测试输入: $\lbrace x=0,y=1\rbrace$, $\lbrace x=2,y=1\rbrace$, $\lbrace x=30,y=15\rbrace$ .

void testme_inf() {          
    int sum = 0;
    int N = sym_input();      
    while (N > 0) {
        sum = sum + N
        N = sym_input();
    }
}

当我们遇到了循环和递归应该怎么办呢？如果循环或递归的终止条件是符号化的，包含循环和递归的符号执行会导致无限数量的路径。比如上面代码中这个例子，这段代码就有无数条执行路径，每条路径的可能性有两种：要么是任意数量的true加上一个false结尾，要么是无穷多数量的true。我们形式化地表示包含n个true条件和1个false条件的路径，其符号化约束如下：

$(\wedge_{i \in [1,n]}N_i > 0) \wedge (N_{n+1} \leq 10)$

其中每个 $N_i$ 都是一个新的符号化值，执行结尾的符号状态是：

$\Big\lbrace N \rightarrow N_{n+1}, sum \rightarrow \sum_{i \in [1,n]} N_i \Big\rbrace$

其实这就是符号执行面临的问题之一，即如何处理循环中的无限多路径。在实际中，有一些方法可以应对，比如对搜索加入限制，要么是限制搜索时间的长短，要么是限制路径数量、循环迭代次数、探索深度等等。

还需要考虑到的一个问题就是，如果符号路径约束包含不能由求解器高效求解的公式怎么办？比如说，如果原本的代码发生变化，把twice函数替换为下述语句：

int twice(int v) {
    return (v*v) % 50;
}

那么符号执行就会产生路径约束 $x_0 \neq (y_0y_0)mod50$ 以及 $x_0 = (y_0y_0)mod50$ 。我们做另外一个假设，如果twice是一个我们得不到源码的函数，也就是我们不知道这个函数有什么功能，那么符号执行会产生路径约束 $x_0 \neq twice(y_0)$ 以及 $x_0 = twice(y_0)$ ，其中twice是一个未解释的函数。这两种情况下，约束求解器都是不能求解这样的约束的，所以符号执行不能产生输入。

其实我们上述介绍的内容，应该属于纯粹的静态符号执行的范畴。我们提出的两个问题，是导致静态符号执行不能够实用的原因之一。符号执行的概念早在1975年[4]就提出了，但是符号执行技术真正得到实用，却是在一种方式提出之后，即混合实际执行和符号执行，称为concolic execution，是真正意义上的动态符号执行。我们会在后面的小节中介绍。

0x3 动态符号执行 Concolic Execution

最早将实际执行(concrete execution)和符号执行(symbolic execution)结合起来的是2005年发表的DART[5]，全称为“Directed Automated Random Testing”(或称concolic testing)，以及2005年发表的CUTE[6]，即“A concolic unit testing engine for C”。

**Concolic执行维护一个实际状态(concrete state)和一个符号化状态(symbolic state)：实际状态将所有变量映射到实际值，符号状态只映射那些有非实际值的变量。Concolic执行首先用一些给定的或者随机的输入来执行程序，收集执行过程中条件语句对输入的符号化约束，然后使用约束求解器去推理输入的变化，从而将下一次程序的执行导向另一条执行路径。**简单地说来，就是在已有实际输入得到的路径上，对分支路径条件进行取反，就可以让执行走向另外一条路径。这个过程会不断地重复，加上系统化或启发式的路径选择算法，直到所有的路径都被探索，或者用户定义的覆盖目标达到，或者时间开销超过预计。

我们依旧以上面那个程序的例子来说明。Concolic执行会先产生一些随机输入，例如{x=22, y=7}，然后同时实际地和符号化地执行程序。这个实际执行会走到第7行的else分支，符号化执行会在实际执行的路径上生成一个路径约束：$x_0 \neq 2y_0$ 。然后Concolic执行会将路径约束的连接词取反，得到新的路径约束 $x_0 = 2y_0$ ，约束求解得到一个新的测试输入{x=2, y=1}，这个新输入就会让执行走向一条不同的路径。之后，Concolic执行会在这个新的测试输入上再同时进行实际的和符号化的执行，执行会取与此前路径不同的分支，即第7行的then分支和第8行的else分支，这时产生的约束就是 $(x_0=2y_0) \wedge (x_0 \leq y_0 + 10)$ ，生成新的测试输入让程序执行没有被执行过的路径。再探索新的路径，就需要将上述新加入的约束条件取反，也就是 $(x_0=2y_0) \wedge (x_0 > y_0 + 10)$ ，通过求解约束得到测试输入{x=30, y=15}，程序会在这个输入上遇到ERROR语句。如此一来，我们就完成了所有3条路径的探索。

PS：注意在这个搜索过程中，其实Concolic执行使用了深度优先的搜索策略。也就是说每次产生新的输入Concolic执行都将执行完整个程序，直到程序结束，然后才返回上一个没有测试的路径约束条件，取反约束条件，得到新的输入，进入新的路径。

这上述过程中，我们从一个实际输入{x=22, y=7}出发，得到第一个约束条件 $x_0 \neq 2y_0$ ，第一次取反得到 $x_0 = 2y_0$ ，从而得到测试输入{x=2, y=1}和新约束 $(x_0=2y_0) \wedge (x_0 \leq y_0 + 10)$ ；第二次取反得到 $(x_0=2y_0) \wedge (x_0 > y_0 + 10)$ ，从而求解出测试输入{x=30, y=15}。

Cristian Cadar在2006年发表EXE，以及2008年发表EXE的改进版本KLEE，对上述Concolic执行的方法做了进一步优化。其创新点主要是在实际状态和符号状态之间进行区分，称之为执行生成的测试（Execution-Generated Testing），简称EGT。这个方法在每次运算前动态检查值是不是都是实际的，如果都是实际的值，那么运算就原样执行，否则，如果至少有一个值是符号化的，运算就会通过更新当前路径的条件符号化地进行。例如，对于我们的例子程序，第17行把y=sym_input()改变成y=10，那么第6行就会用实际参数10去调用函数twice，并实际执行。然后第7行变成if(20==x)，符号执行若走then路径，则加入约束x=20；对条件进行取反就可以走else路径，约束是x≠20。在then路径上，第8行变成if(x>20)，那么该if的then路径就不能走了，因为此时有约束x=20。简言之，EGT本质上还是将实际执行与符号执行相结合，通过路径取反探索所有可能路径。

正是因为concolic执行的出现，让传统静态符号执行遇到的很多问题能够得到解决——那些符号执行不好处理的部分、求解器无法求解的部分，用实际值替换就好了。使用实际值，可以让因外部代码交互和约束求解超时造成的不精确大大降低，但付出的代价就是，会有丢失路径的缺陷，牺牲了路径探索的完全性。我们举一个例子来说明这一点。假设我们原始例子程序做了改动，即把twice函数的定义改为返回(v*v)%50。假设执行从随机输入{x=22, y=7}开始，if(x==z)条件取反生成路径约束 $x_0 \neq (y_0y_0)mod50$ 。因为约束求解器无法求解非线性约束，所以concolic执行的应对方法是，把符号值用实际值替换，此处会把 $y_0$ 的值替换为7，这就将程序约束简化为 $x_0 \neq 49$ 。通过求解这个约束，可以得到输入{x=49, y=7}，走到一个此前没有走到的路径。传统静态符号执行是无法做到这一步的。但是，在这个例子中，我们无法生成路径true-false的输入，即约束 $(x_0 \neq (y_0y_0)mod50) \wedge (x_0 \leq y_0 + 10)$ ，因为 $y_0$ 的值已经实际化了，这就造成了丢失路径的问题，造成不完全性。

然而总的来说，Concolic执行的方法是非常实用的，有效解决了遇到不支持的运算以及应用与外界交互的问题。比如调用库函数和系统调用的情况下，因为库和系统调用无法插桩，所以这些函数相关的返回值会被实际化，以此获得简化的程序约束。

0x4 面临挑战&解决方案

符号执行曾经遇到过很多问题，使其难以应用在真实的程序分析中。经过研究者的不懈努力，这些问题多多少少得到了解决，由此也产生了一大批优秀的学术论文。这一部分将简单介绍其中的一些关键挑战以及对应的解决方案。

1.路径爆炸(Path Explosion)

由于在每一个条件分支都会产生两个不同约束，符号执行要探索的执行路径依分支数指数增长。在时间和资源有限的情况下，应该对最相关的路径进行探索，这就涉及到了路径选择的问题。通过路径选择的方法缓解指数爆炸问题，主要有两种方法：

1）使用启发式函数对路径进行搜索，目的是先探索最值得探索的路径；

2）使用一些可靠的程序分析技术减少路径探索的复杂性。

启发式搜索是一种路径搜索策略，比深度优先或者宽度优先要更先进一些。大多数启发式的主要目标在于获得较高的语句和分支的覆盖率，不过也有可能用于其他优化目的。最简单的启发式大概是随机探索的启发式，即在两边都可行的符号化分支随机选择走哪一边。还有一个方法是，使用静态控制流图（CFG）来指导路径选择，尽量选择与未覆盖指令最接近的路径。另一个方法是符号执行与进化搜索相结合，其fitness function用来指导输入空间的搜索，其关键就在于fitness function的定义，例如利用从动态或静态分析中得到的实际状态(concrete state)信息或者符号信息来提升fitness function。

用程序分析和软件验证的思路去减少路径探索的复杂性，也是一种缓解路径爆炸问题的方式。一个简单的方法是，通过静态融合减少需要探索的路径，具体说来就是使用select表达式直接传递给约束求解器，但实际上是将路径选择的复杂性传递给了求解器，对求解器提出了更高的要求。还有一种思路是重用，即通过缓存等方式存储函数摘要，可以将底层函数的计算结果重用到高级函数中，不需要重复计算，减小分析的复杂性。还有一种方法是剪枝冗余路径，RWset技术的关键思路就是，如果程序路径与此前探索过的路径在同样符号约束的情况下到达相同的程序点，那么这条路径就会从该点继续执行，所以可以被丢弃。

2.约束求解(Constraint Solving.)

符号执行在2005年之后的突然重新流行，一大部分原因是因为求解器能力的提升，能够求解复杂的路径约束。但是约束求解在某种程度上依然是符号执行的关键瓶颈之一，也就是说符号执行所需求的约束求解能力超出了当前约束求解器的能力。所以，实现约束求解优化就变得十分重要。这里主要介绍两种优化方法：不相关约束消除，增量求解。

a.不相关约束消除(Irrelevant constraint elimination)

在符号执行的约束生成过程中，尤其是在concolic执行过程中，通常会通过条件取反的方式增加约束，一个已知路径约束的分支谓词会取反，然后由此产生的约束集会检查可满足性以识别另一条路径是否可行。一个很重要的现象是，一个程序分支通常只依赖一小部分程序变量，所以我们可以尝试从当前路径条件中移除与决定当前分支结果不相关的约束。例如，当前的路径条件是 $(x+y>10) \wedge (z>0) \wedge (y<12) \wedge (z−x=0)$ 假如我们想对y<12这个分支条件探索新路径，可以通过约束 $(x+y>10) \wedge (z>0) \wedge \neg (y<12)$ 求解新的输入， $\neg (y<12)$ 是取反的条件分支，我们可以去掉对z的约束，是因为z对 $\neg (y<12)$ 的分支是不会有影响的。减小的约束集会给出x和y的新值，我们用此前执行的z值就可以生成新输入了。如果更形式化地说，算法会计算在取反条件所依赖的所有约束的传递闭包。

（其实沃觉得是有影响的，x=z，z>0，那不就是x>0吗，如果去掉x-z=0，相当于去掉x>0，x会通过第一项约束条件影响y啊，不是吗？所以这个栗子可能不恰当，这里理解不相关约束消除的概念就行了，如有不同意见欢迎指正）

b.增量求解(Incremental solving)

本质上也是利用重用的思想。符号执行中生成的约束集有一个重要特性，就是表示为程序源代码中的静态分支的固定集合。所以，很多路径有相似的约束集，可以有相似的解决方案。通过重用以前相似请求的结果，可以利用这种特性来提升约束求解的速度，这种方法在CUTE和KLEE中都有实现。举个例子来说明，在KLEE中，所有的请求结果都保存在缓存中，该缓存将约束集映射到实际变量赋值。例如，缓存中的一个映射可能是：

$(x+y<10) \wedge (x>5) \Rightarrow \lbrace x=6,y=3 \rbrace$

使用这些映射，KLEE可以迅速解答一些相似的请求类型，包括已经缓存的约束集的子集和超集。比如对于请求$(x+y<10) \wedge (x>5) \wedge (y \geq 0)$ ，KLEE可以迅速检查{x=6,y=3}是一个可行的答案。这样就可以让求解过程加快很多。

3.内存建模(Memory Modeling)

程序语句转换为符号约束的精度对符号执行能实现的覆盖率以及约束求解的可伸缩性有很大影响。例如，使用数学整数(actual mathematical integers)去近似去代替固定宽度的整数变量，这样的内存模型可能会更有效率，但另一方面，根据诸如算术溢出之类的极端情况，可能导致代码分析不精确-这可能会导致符号执行遗漏路径或探索不可行的路径。

另外一个问题是指针。在访问内存的时候，内存地址（指针）用来引用一个内存单元，当这个地址的引用来自于用户输入时，内存地址就成为了一个表达式。当符号化执行时，我们必须决定什么时候将这个内存的引用进行实际化。一个可靠的策略是，考虑为从任何可能满足赋值的加载，但这个可能值的空间很大，如果实际化不够精确，会造成代码分析的不精确。

还有一个是别名问题，即地址别名导致两个内存运算引用同一个地址，比较好的方法是进行别名分析，事先推理两个引用是否指向相同的地址，但这个步骤要静态分析完成。KLEE使用了别名分析和让SMT考虑别名问题的混合方法。而DART和CUTE压根没解决这个问题，只处理线性约束的公式，不能处理一般的符号化引用。

符号化跳转也是一个问题，主要是switch这样的语句，常用跳转表实现，跳转的目标是一个表达式而不是实际值。以往的工作用三种处理方法。

1）使用concolic执行中的实际化策略，一旦跳转目标在实际执行中被执行，就可以将符号执行转向这个实际路径，但缺陷是实际化导致很难探索完全的状态空间，只能探索已知的跳转目标。

2）使用SMT求解器。当我们到达符号跳转时，假设路径谓词为 $\Pi$ ，跳转到e，我们可以让SMT求解器找到符合 $\Pi \wedge e$ 的答案。但是这种方案相比其他方案效率会低很多。

3）使用静态分析，推理整个程序，定位可能的跳转目标。

实际中，源代码的间接跳转分析主要是指针分析。二进制的跳转静态分析推理在跳转目标表达式中哪些值可能被引用。例如，函数指针表通常实现为可能的跳转目标表。

4.处理并发(Handling Concurrency)

大型程序通常是并发的。因为这种程序的内在特性，动态符号执行系统可以被用来高效地测试并发程序，包括复杂数据输入的应用、分布式系统以及GPGPU程序。

0x5 发展脉络(至2017)

本节仍然摘录自r1ce的文章，主要是以时间的顺序梳理符号执行技术的发展脉络，同时对值得关注的项目和论文做一个小小总结和推荐。

符号执行最初提出是在70年代中期，主要描述的是静态符合执行的原理，到了2005年左右突然开始重新流行，是因为引入了一些新的技术让符号执行更加实用。Concolic执行的提出让符号执行真正成为可实用的程序分析技术，并且大量用于软件测试、逆向工程等领域。在2005年作用涌现出很多工作，如DART[5]、CUTE[6]、EGT/EXE[7]、CREST[8]等等，但真正值得关注和细读的，应该是2008年Cristian Cadar开发的KLEE[3]。KLEE可以说是源代码符号执行的经典作品，又是开源的，后来的许多优秀的符号执行工具都是建立在KLEE的基础上，因此我认为研究符号执行，KLEE的文章是必读的。

基于二进制的符号执行工具则是2009年EPFL的George Candea团队开发的S2E[9]最为著名，其开创了选择符号执行这种方式。2012年CMU的David Brumley团队提出的Mayhem[10]则采用了混合offline和online的执行方式。2008年UC Berkeldy的Dawn Song团队提出的BitBlaze[11]二进制分析平台中的Rudder模块使用了online的执行方式，也值得一看。总之，基于二进制的符号执行工作了解这三个就足够了。其中，S2E有开源的一个版本，非常值得仔细研究。最近比较火的angr[12]，是一个基于Python实现的二进制分析平台，完全开源且还在不断更新，其中也实现了多种不同的符号执行策略。

在优化技术上，近几年的两个工作比较值得一看其一是2014年David Brumley团队提出的路径融合方法，叫做Veritesting[13]，是比较重要的工作之一，angr中也实现了这种符号执行方式。另一个是2015年Stanford的Dawson Engler（这可是Cristian Cadar的老师）团队提出的Under-Constrained Symbolic Execution[14]。

另外，近年流行的符号执行与fuzzing技术相结合以提升挖掘漏洞效率，其实早在DART和2012年微软的SAGE[15]工作中就已经有用到这种思想，但这两年真正火起来是2016年UCSB的Shellphish团队发表的Driller[16]论文，称作符号辅助的fuzzing（symbolic-assisted fuzzing），也非常值得一看。

0x6 总结

符号执行已是一种有效的程序测试技术，它提供了一种自动生成"触发软件错误的输入"的方法，这些错误从底层程序崩溃到高层语义特性不等。符号执行技术可以用于测试例的自动生成，也可以用于源代码安全性的检测。这两项工作的成效都十分依赖于约束求解器的性能，同时还受硬件设备处理能力的影响。

虽然需要更多的研究来提高符号执行的代码覆盖率，测试精度，分析效率等等指标，但是事实证明，现有工具可以有效地测试和发现各种软件中的错误，从低级网络和操作系统代码到高级应用程序代码，不一而足。

从实用性的角度来说：

（2018年）现有的符号执行工具，在开源方面，主要还是基于KLEE项目的。可见对于KLEE项目的深入理解，将有助于我们打造更加高效的工具。有了高效的工具，就能够使得我们一边学习理论，一遍验证，从而走上高速公路。Inception工具是就ARM架构，而对于路由器中常使用的MIPS架构，现在应该还尚未有类似的符号执行工具发布（如果已经由类似工具，欢迎读者留言）。其中，基于IDA的脚本工具bugscam，经过揭秘路由器0DAY漏洞的作者修改之后，也能够支持分析MIPS架构的漏洞了。然而，其误报率非常之高，该工具报告的漏洞基本都不可用。因此，如何基于上述符号执行的思想，结合IDA工具中强大的反汇编能力，开发也具有符号执行功能的MIPS架构漏洞分析工具，相信也是非常有价值的。

0x7 To Learn More

摘自r1ce的文章：

对于符号执行入门，有两篇文章可以参考。其一是2010年David Brumley团队在S&P会议上发表的《All You Ever Wanted to Know about Dynamic Taint Analysis and Forward Symbolic Execution (but Might Have Been Afraid to Ask)》[1]。这篇文章同时介绍了动态污点分析和前向符号执行的基本概念，作者构造了一种简化的中间语言，用来形式化地描述这两种程序分析技术的根本原理。其二是2011年Cristian Cadar发表在ACM通讯上的一篇短文《Symbolic execution for software testing: three decades later》[2]，以较为通俗的语言和简单的例子阐述了符号执行的基本原理，并介绍了符号执行技术的发展历程和面临挑战。

其实这两篇文章的作者都是二进制分析领域大名鼎鼎的人物，卡内基梅隆的David Brumley是AEG的提出者，其带领团队是DARPA CGC比赛的第一名；英国帝国理工的Cristian Cadar则是符号执行引擎KLEE[3]的作者——KLEE在符号执行领域的地位不言而喻。这两篇文章各有千秋：前者更加学术化一些，用中间语言进行的形式化描述有些晦涩难懂，但对于进一步研究符号执行引擎的源码很有帮助；后者则更通俗一些，有助于初学者的理解，且对于符号执行的发展脉络有更多的介绍。

Q&A:

A:如何通俗易懂的总结符号执行技术？

Q:符号执行是一种白盒静态代码分析技术，用符号表示程序的输入，根据分析程序语义得到的约束条件，去求解能得到你所希望的程序输出所需要的输入，的一种方法。更容易理解的说法可以参开0x1第一段。

Q:路径约束PC到底长什么样子？

A:一长串约束条件，比如0x2中的示例： $(\wedge_{i \in [1,n]}N_i > 0) \wedge (N_{n+1} \leq 10)$

Q:约束求解器是怎么运作的？

A:

Q:Concolic执行的出现，让传统静态符号执行遇到的很多问题能够得到解决（解决了哪些问题？怎么解决的？）

A:Concolic执行的方法有效解决了遇到不支持约束求解的运算以及应用与外界交互的问题；具体方法就是，那些传统静态符号执行不好处理的部分、求解器无法求解的部分，用实际值替换就好了

Q:Concolic执行和传统静态符号执行哪里不同？

A:我的理解是，1.传统静态符号执行使用符号表示变量，比如符号状态 $\sigma$ 中存在变量x的映射$x \rightarrow x_0$，2.使用约束求解器判定哪条分支可行，并根据预先设计的路径调度策略实现对该过程所有路径的遍历分析，最后输出每条可执行路径的分析结果，即每条路径对应的输入和输出；

而Concolic执行来说，1.它使用具体数值作为输入来模拟执行程序代码，2.从当前路径的分支语句的谓词中搜集所有符号约束。然后修改该符号约束内容构造出一条新的可行的路径约束，并用约束求解器求解出一个可行的新的具体输入，接着符号执行引擎对新输入值进行一轮新的分析。通过使用这种输入迭代产生变种输入的方法分析程序。

参考文章：

K0rz3n：https://www.k0rz3n.com/2019/02/28/简单理解符号执行技术/

r1ce：https://zhuanlan.zhihu.com/p/26927127

符号执行——从入门到上高速：https://www.anquanke.com/post/id/157928

http://pwn4.fun/2017/03/20/符号执行基础/

[2]* Symbolic execution for software testing: three decades later：https://people.eecs.berkeley.edu/~ksen/papers/cacm13.pdf

[1] Schwartz E J, Avgerinos T, Brumley D. All You Ever Wanted to Know about Dynamic Taint Analysis and Forward Symbolic Execution (but Might Have Been Afraid to Ask) [C]// Security & Privacy. DBLP, 2010:317-331.

[2] Cadar C, Sen K. Symbolic execution for software testing: three decades later[M]. ACM, 2013.

[3] C. Cadar, D. Dunbar, and D. Engler. KLEE: Unassisted and Automatic Generation of High-Coverage Tests for Complex Systems Programs. In Proceedings of the 8th USENIX Symposium on Operating Systems Design and Implementation (OSDI’08), volume 8, pages 209–224, 2008.

[4] R. S. Boyer, B. Elspas, and K. N. Levitt. SELECT – a formal system for testing and debugging programs by symbolic execution. SIGPLAN Not., 10:234–245, 1975.

[5] P. Godefroid, N. Klarlund, and K. Sen. DART: Directed Automated Random Testing. In PLDI’05, June 2005.

[6] K. Sen, D. Marinov, and G. Agha. CUTE: A concolic unit testing engine for C. In ESEC/FSE’05, Sep 2005.

[7] C. Cadar, V. Ganesh, P. M. Pawlowski, D. L. Dill, and D. R. Engler. EXE: Automatically Generating Inputs of Death. In Proceedings of the 13th ACM Conference on Computer and Communications Security, pages 322–335, 2006.

[8] J. Burnim and K.Sen,“Heuristics for scalable dynamic test generation,” in Proc. 23rd IEEE/ACM Int. Conf. Autom. Software Engin., 2008, pp. 443–446.

[9] V. Chipounov, V. Georgescu, C. Zamfir, and G. Candea. Selective Symbolic Execution. In Proceedings of the 5th Workshop on Hot Topics in System Dependability, 2009.

[10] S. K. Cha, T. Avgerinos, A. Rebert, and D. Brumley. Unleashing Mayhem on Binary Code. In Proceedings of the IEEE Symposium on Security and Privacy, pages 380–394, 2012.

[11] Song D, Brumley D, Yin H, et al. BitBlaze: A New Approach to Computer Security via Binary Analysis[C]// Information Systems Security, International Conference, Iciss 2008, Hyderabad, India, December 16-20, 2008. Proceedings. DBLP, 2008:1-25.

[12] Yan S, Wang R, Salls C, et al. SOK: (State of) The Art of War: Offensive Techniques in Binary Analysis[C]// Security and Privacy. IEEE, 2016:138-157.

[13] T. Avgerinos, A. Rebert, S. K. Cha, and D. Brumley. Enhancing Symbolic Execution with Veritesting. pages 1083–1094, 2014.

[14] D. a. Ramos and D. Engler. Under-Constrained Symbolic Execution: Correctness Checking for Real Code. In Proceedings of the 24th USENIX Security Symposium, pages 49–64, 2015.

[15] P. Godefroid, M. Y. Levin, and D. Molnar. SAGE: Whitebox Fuzzing for Security Testing. ACM Queue, 10(1):20, 2012.

[16] N. Stephens, J. Grosen, C. Salls, A. Dutcher, R. Wang, J. Corbetta, Y. Shoshitaishvili, C. Kruegel, and G. Vigna. Driller: Augmenting Fuzzing Through Selective Symbolic Execution. In Proceedings of the Network and Distributed System Security Symposium, 2016.