Graph Neural Network
slides: http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML2020/GNN.pdf
Introduction
定义
GNN 图神经网络 就是把图作为神经网络的输入,识别图结构,提取图信息,或生成特定结构的图的神经网络模型。
这里的“图”是指图论中的图,即由边和节点构成的图,比如下图中化学分子结构图,二叉树、台湾省地铁线路图:
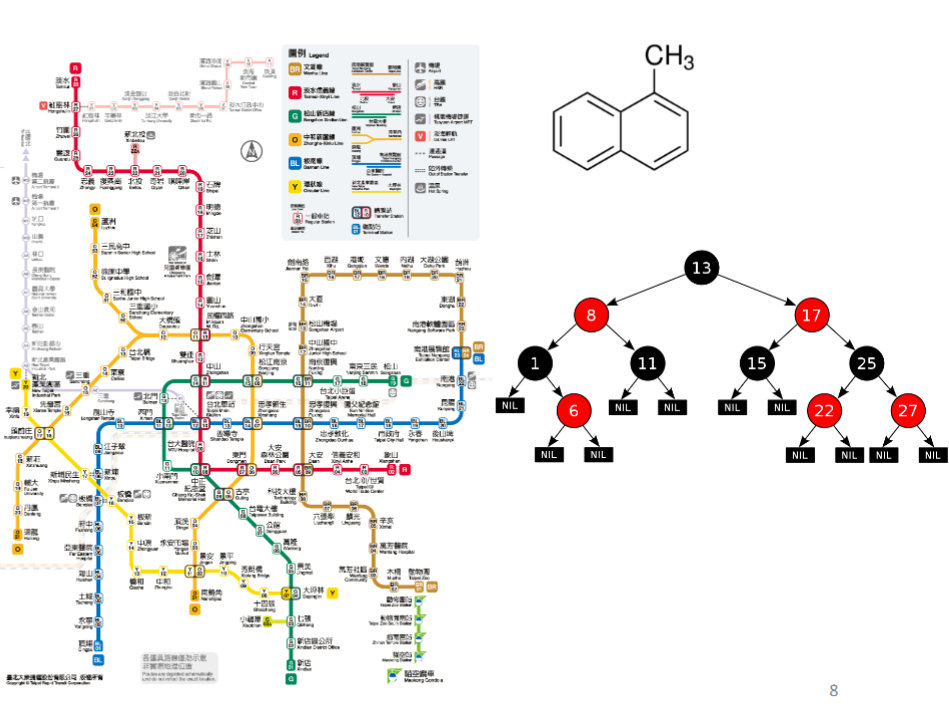
训练GNN将遇到的问题
如何利用图的结构和节点之间的关系信息训练模型(即模型如何吃Graph)?
如果图非常大怎么办?
图非常大的时候通常我们没有所有node的label information,怎么办?
首先第一个问题,model如何吃graph的问题:
convolution?
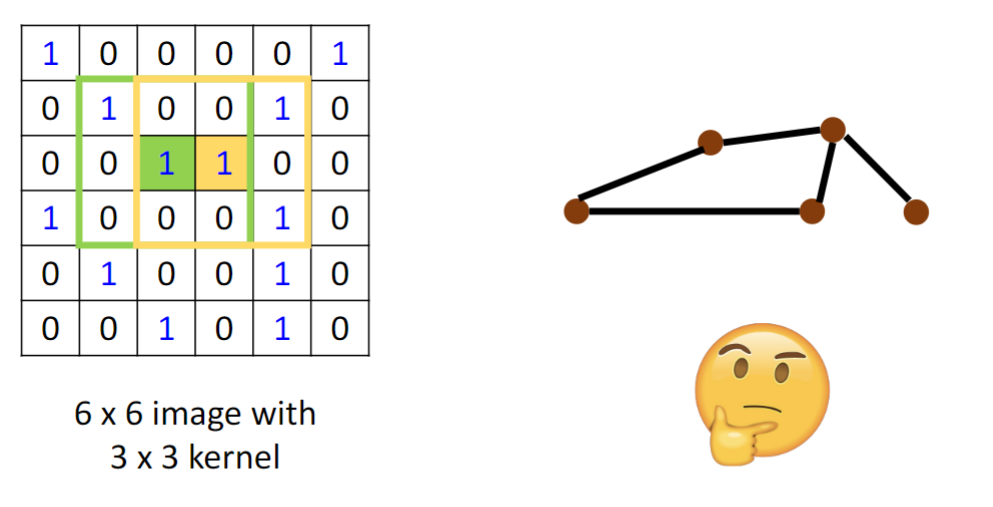
如何把CNN里卷积的方法移植到图神经网络?
所以如何使用convolution将node 嵌入到一个feature space?
- Solution 1: Generalize the concept of convolution (corelation) to graph >> Spatial-based convolution
- Solution 2: Back to the definition of convolution in signal processing >> Spectral-based convolution
Roadmap
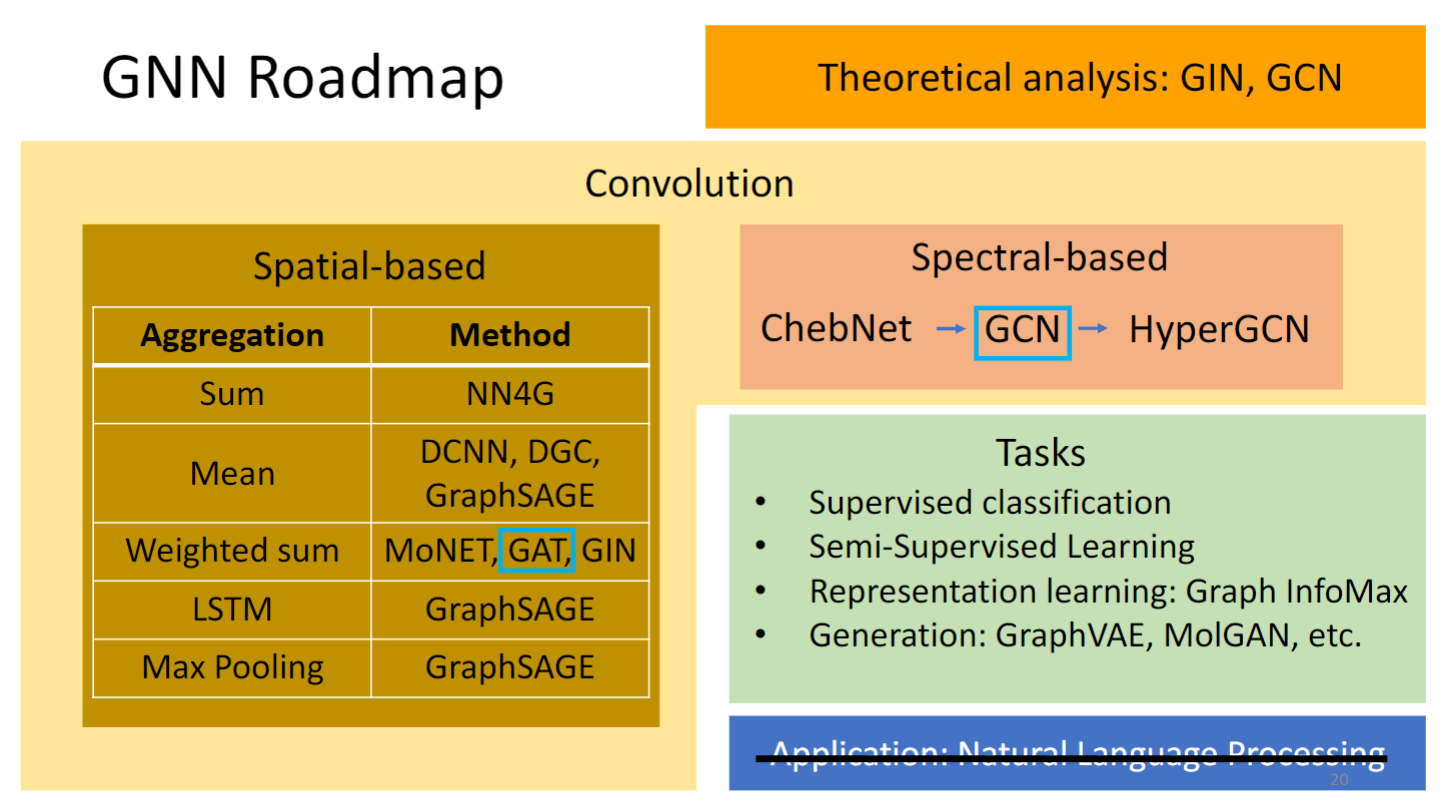
本节会讲的是:GAT和GCN.
Tasks, Dataset, and Benchmark
Tasks
- Semi-supervised node classification
- Regression
- Graph classification
- Graph representation learning
- Link prediction
Common dataset
- CORA: citation network. 2.7k nodes and 5. 4k links
- TU-MUTAG: 188 molecules with 18 nodes on average
这些benchmark的task和dataset用来评估GNN模型好坏,建议先看完下一节Spatial-based GNN再回来看这些任务

这个数据集通过某种算法将原始MNIST和CIFAR10的图片转成graph,GNNs的任务就是graph classification
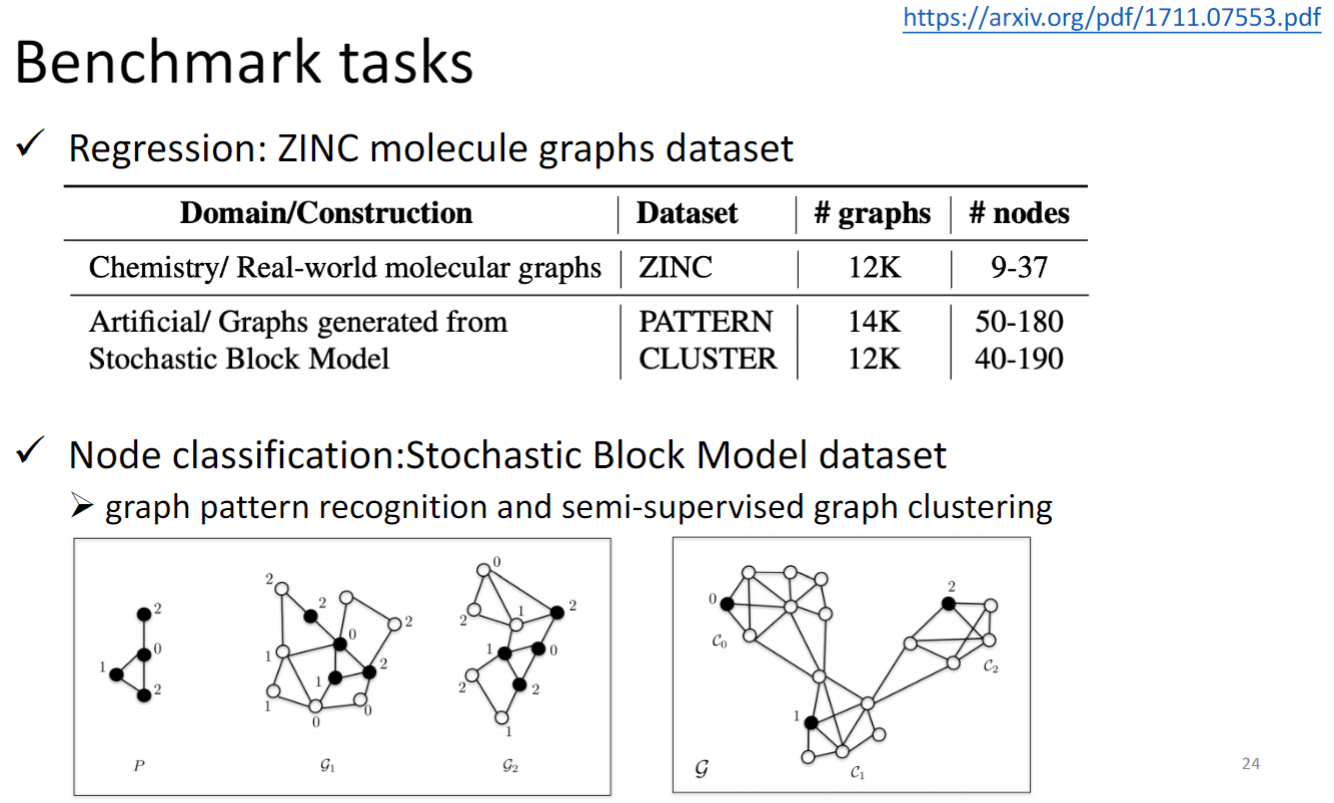
ZINC 是通过分子graph 计算分子溶解度,属于回归任务
Stochastic Block Model dataset 是给出一个pattern,model要是别这个pattern是否出现在一个graph中
这个数据集还可以做另一个任务:每个图由不同的community或者说cluster,model要判断一个node属于哪个cluster
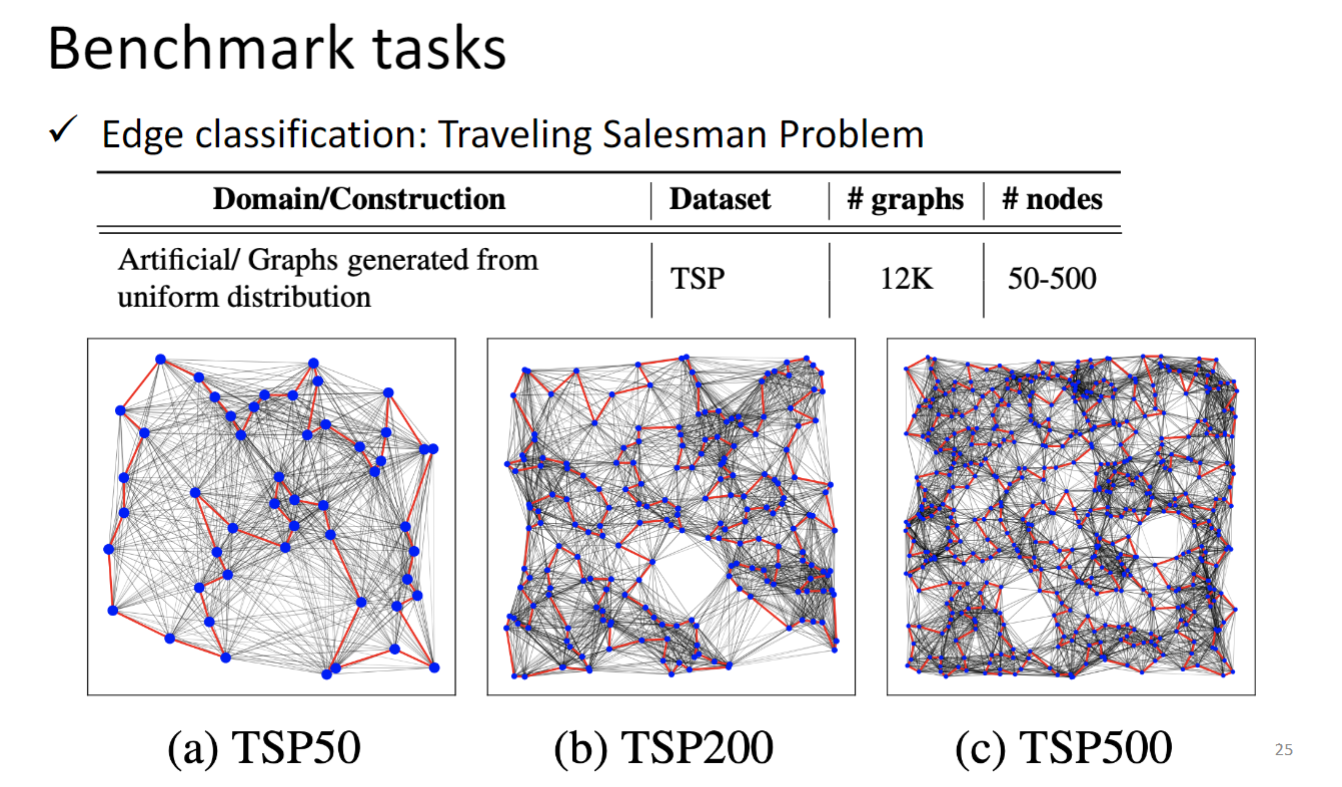
TSP 路径规划问题,就不用赘述了.
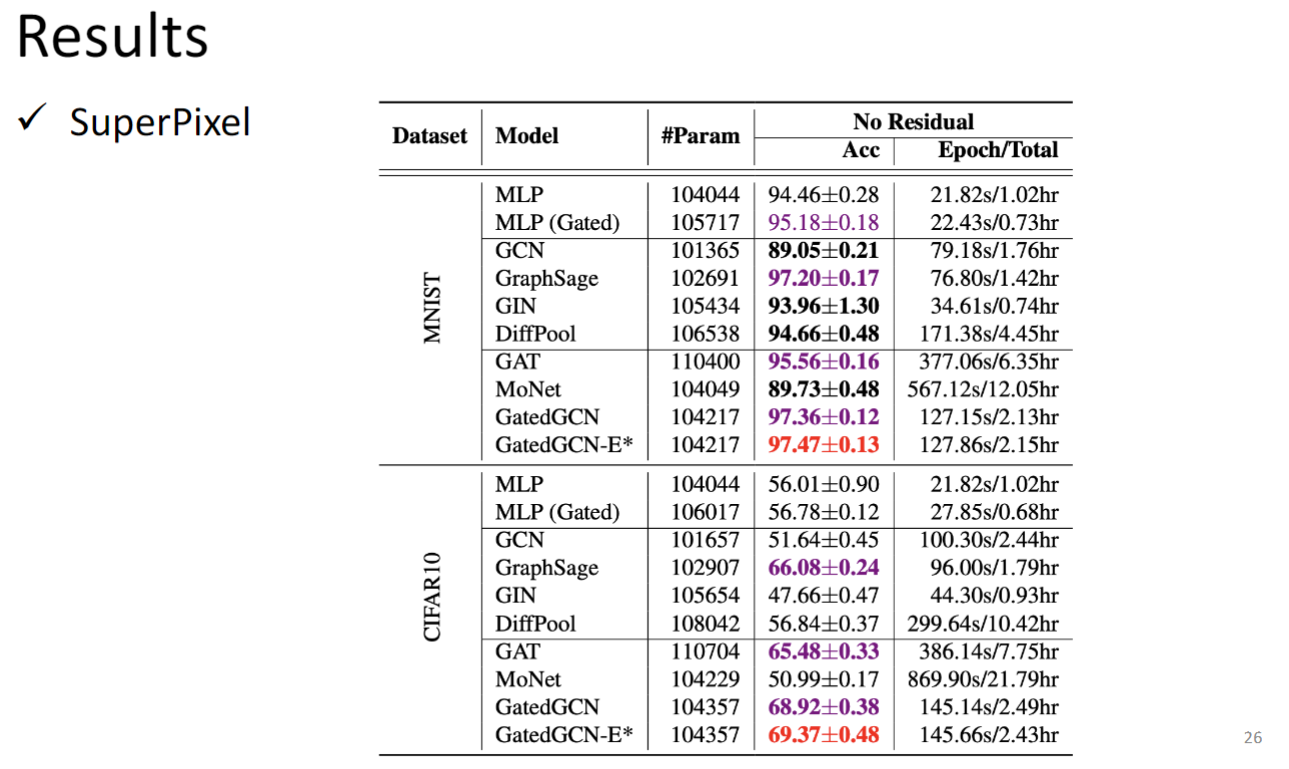
Spatial-based GNN
复习一下CNN的Convolution:
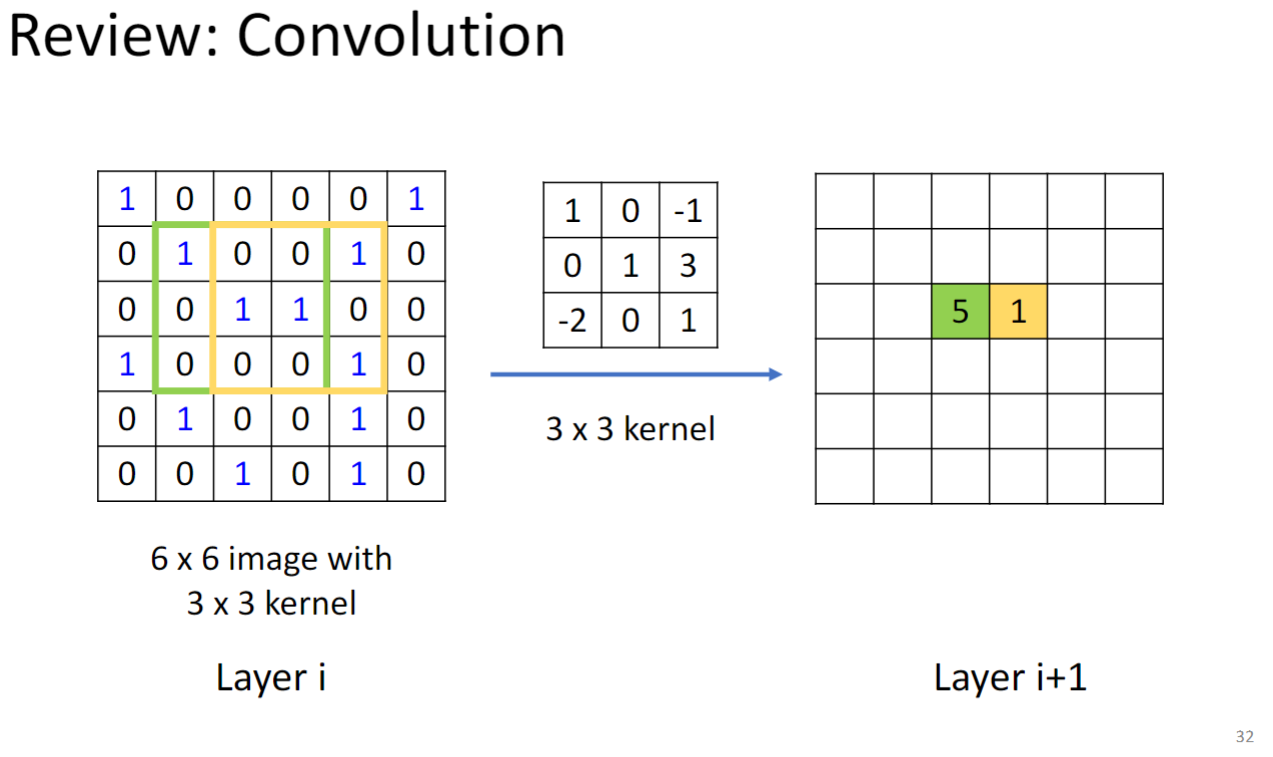
CNN在layer i上通过kernel计算feature得到layer i+1层的feature,类比到Graph上:
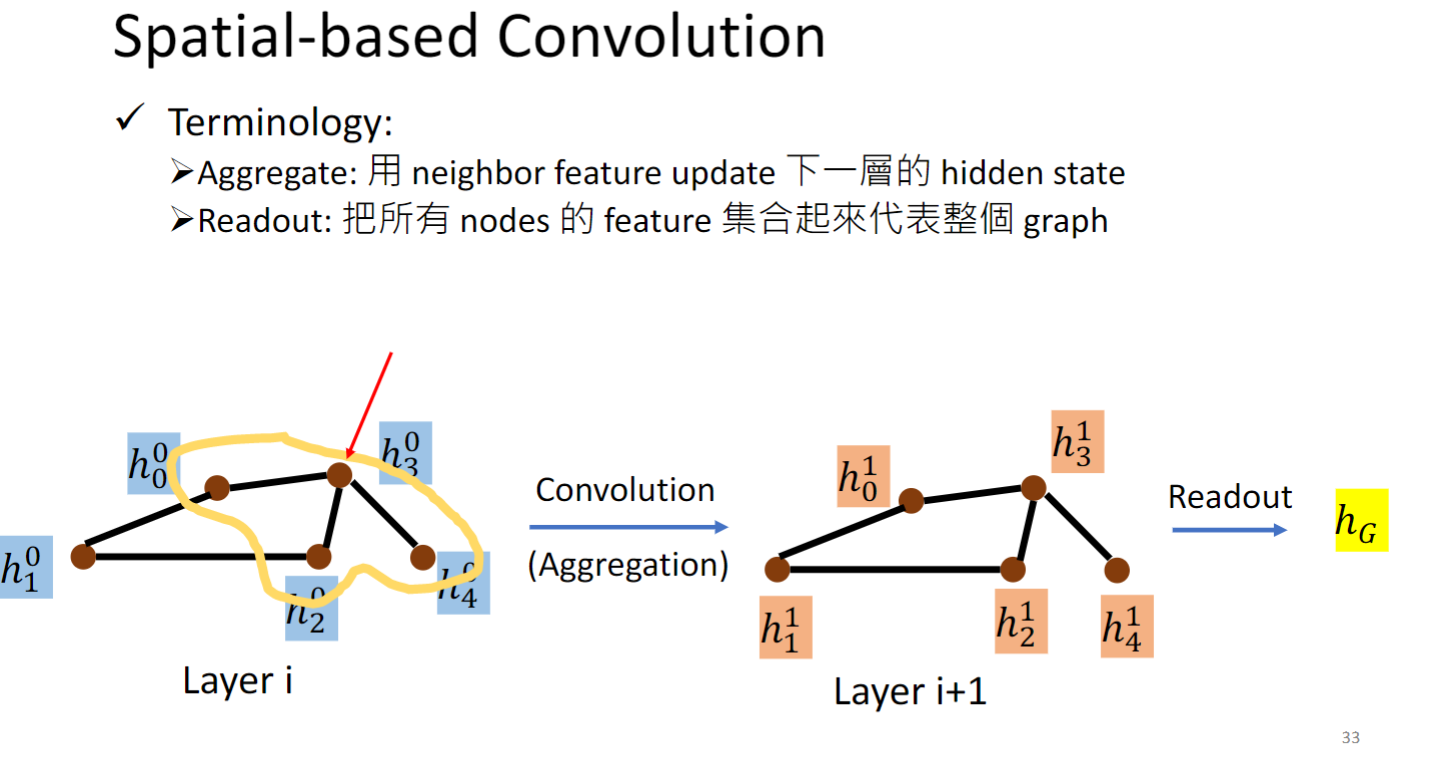
以 为例,0表示第0 layer,3表示第3个node,它的邻居是黄色圈起来的三个几点,我们就用这三个邻居的hidden feature 来算出下一层的hidden layer,这一招叫做Aggregation.
如果我们还想同时计算出某一层整个graph的representation,预测一个分子是否会变异,就把所有node的feature集合起来,这个操作叫做readout.
NN4G(Neural Networks for Graph)
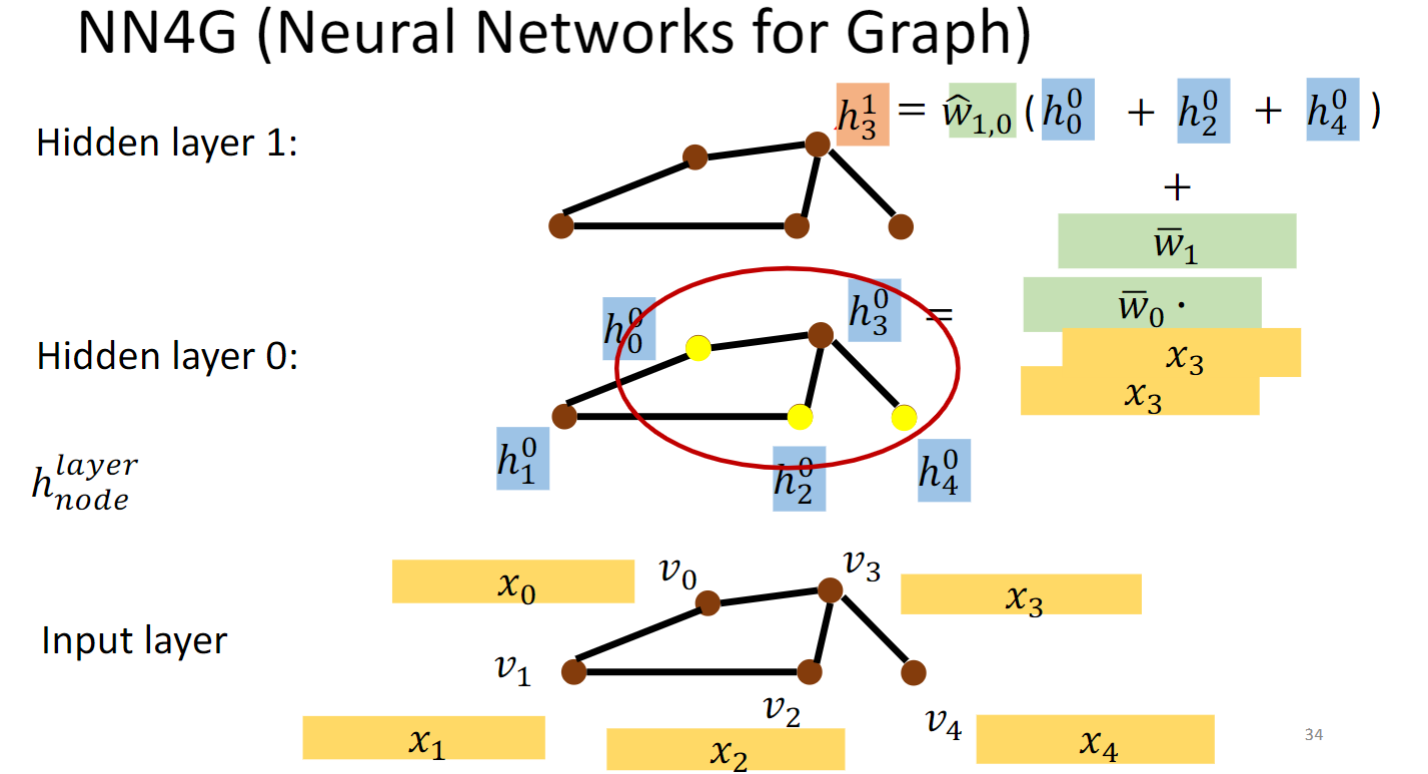
NN4G这个模型的做法如上图所示,每个节点v都用一个特征向量x表示,对每个节点做embedding,即乘一个矩阵w,得到h,然后从一个hidden layer到下一个hidden layer做Aggregation,具体做法就是将一个节点的邻居的h加起来乘上一个w,就得到这个节点在下一个hidden layer的h.
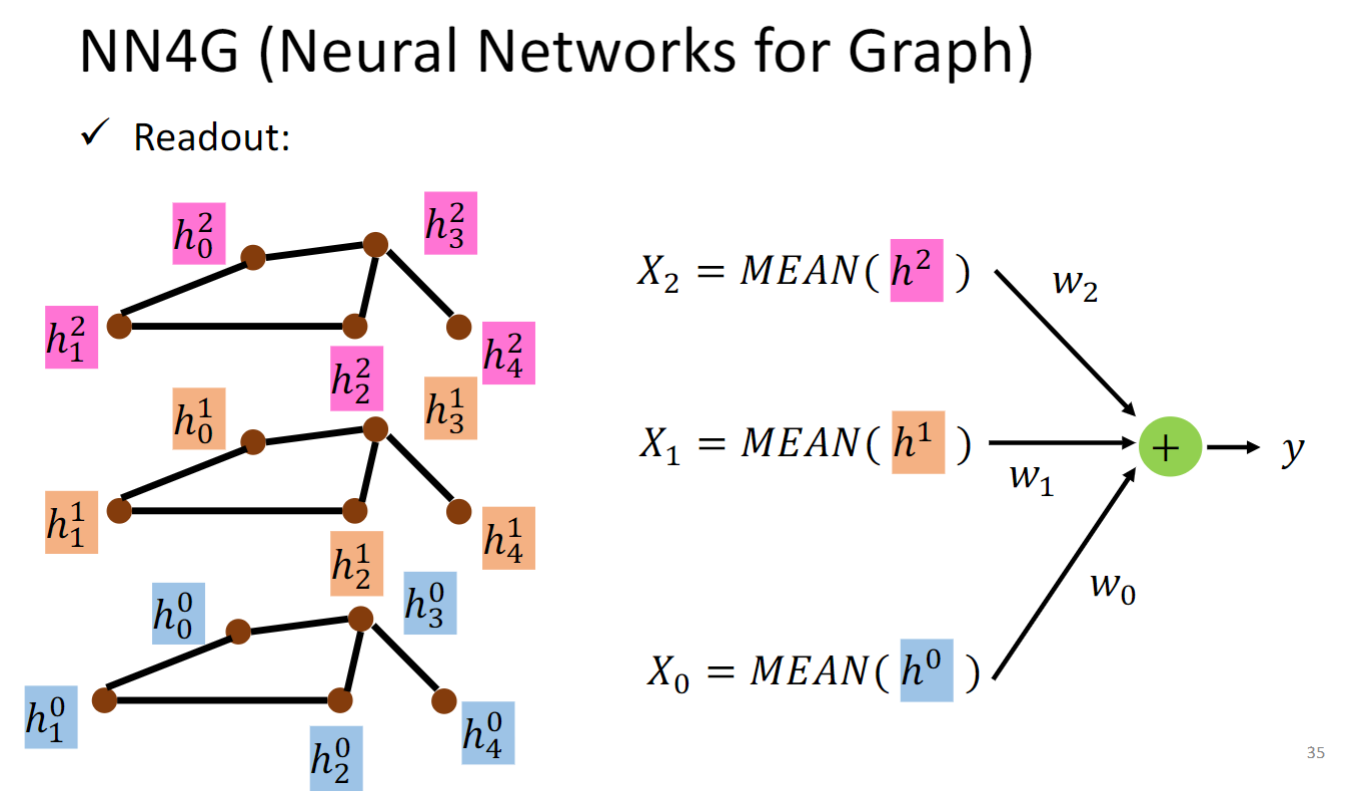
NN4G这个模型Readout的做法如上图所示,无需多言.
DCNN(Diffusion-Convolution Neural Network)
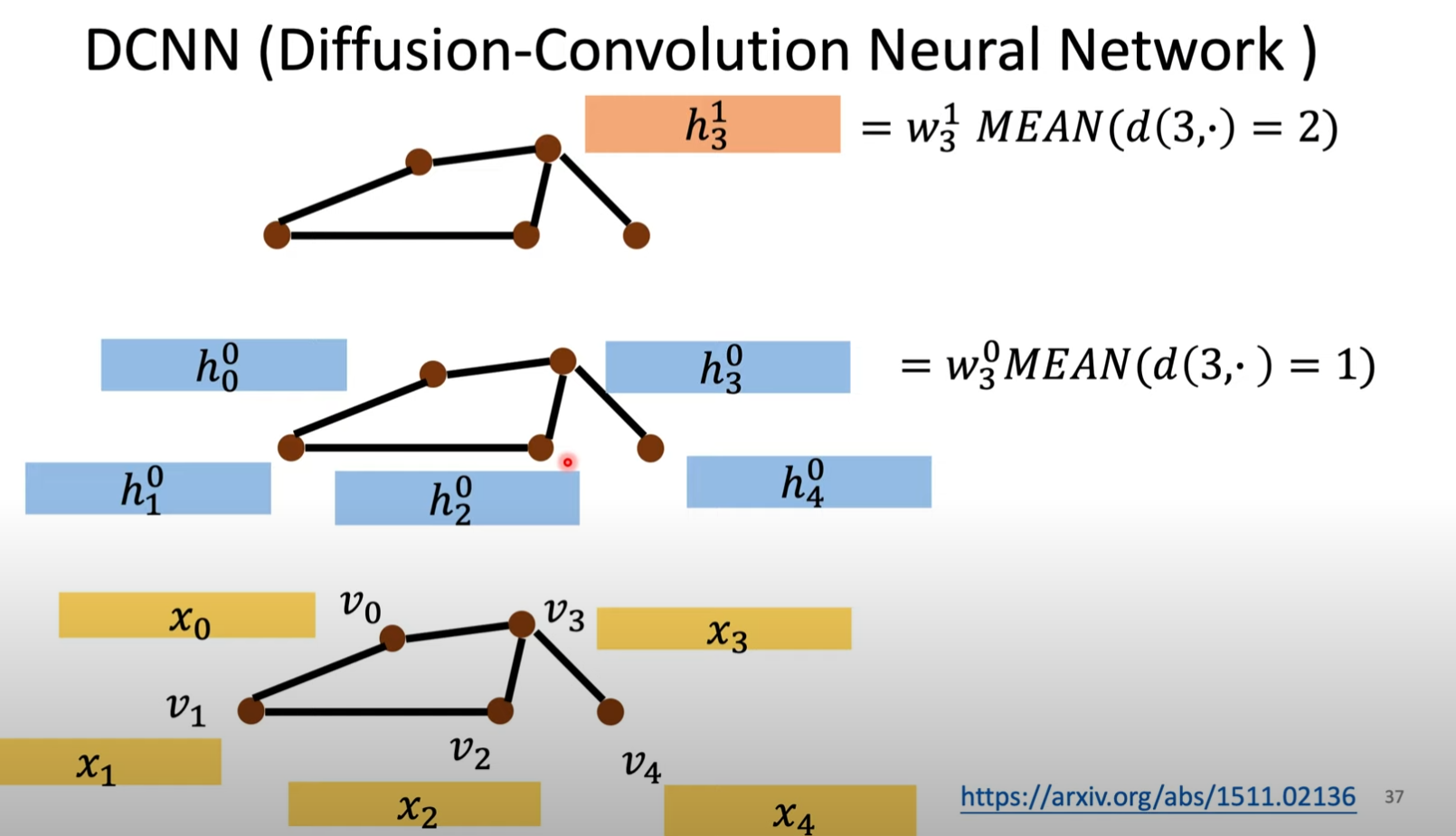
这个模型的Aggregation的做法是:每一层都从第一层计算得来,算是这样算的:
这是说和距离为1的节点取平均,乘上一个权重矩阵,即节点v0 v2 v4。算完每个节点以后得到第一层的h。
这是说和距离为2的节点取平均,乘上一个权重矩阵,即节点v1 v3。算完每个节点以后得到第二层的h。
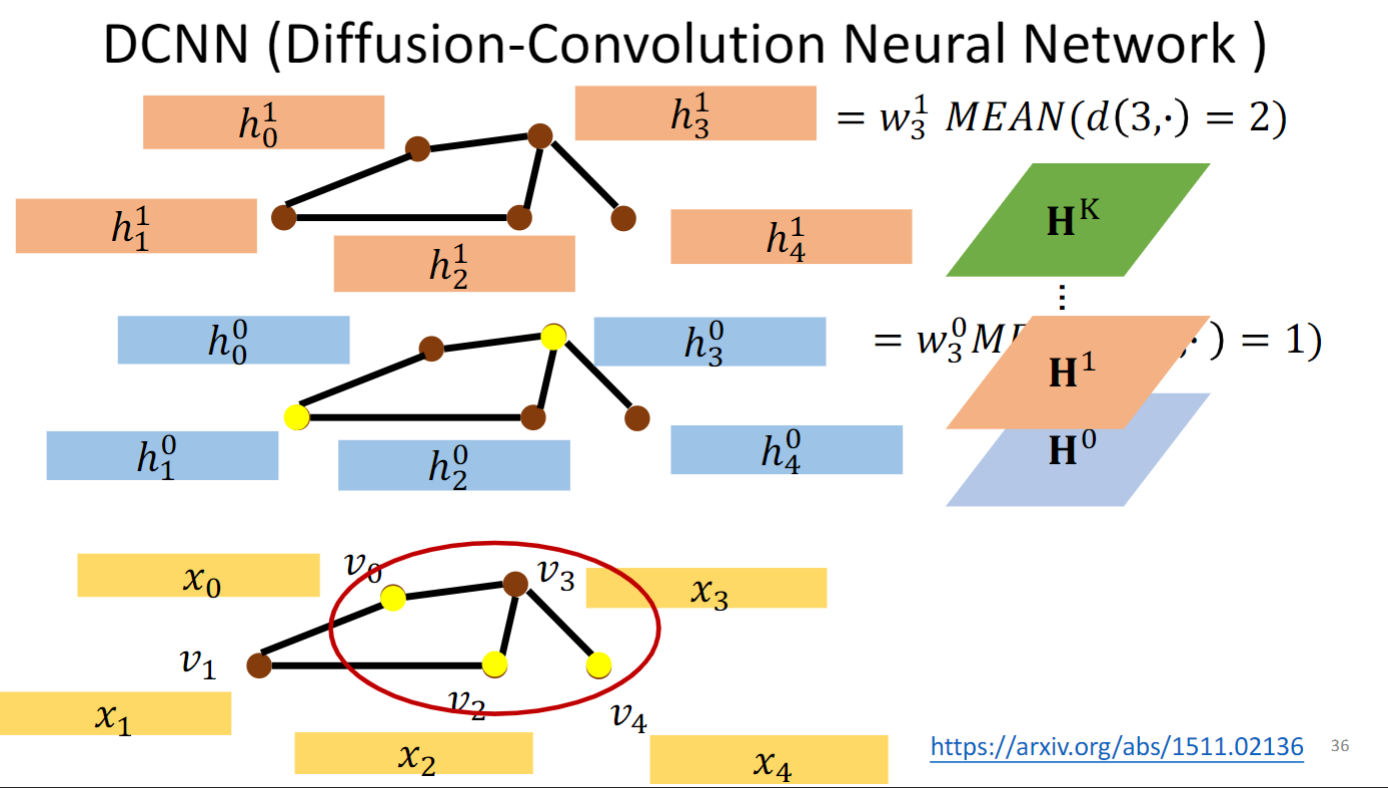
是将每层的h一行一行放在一起,叠成一个矩阵.
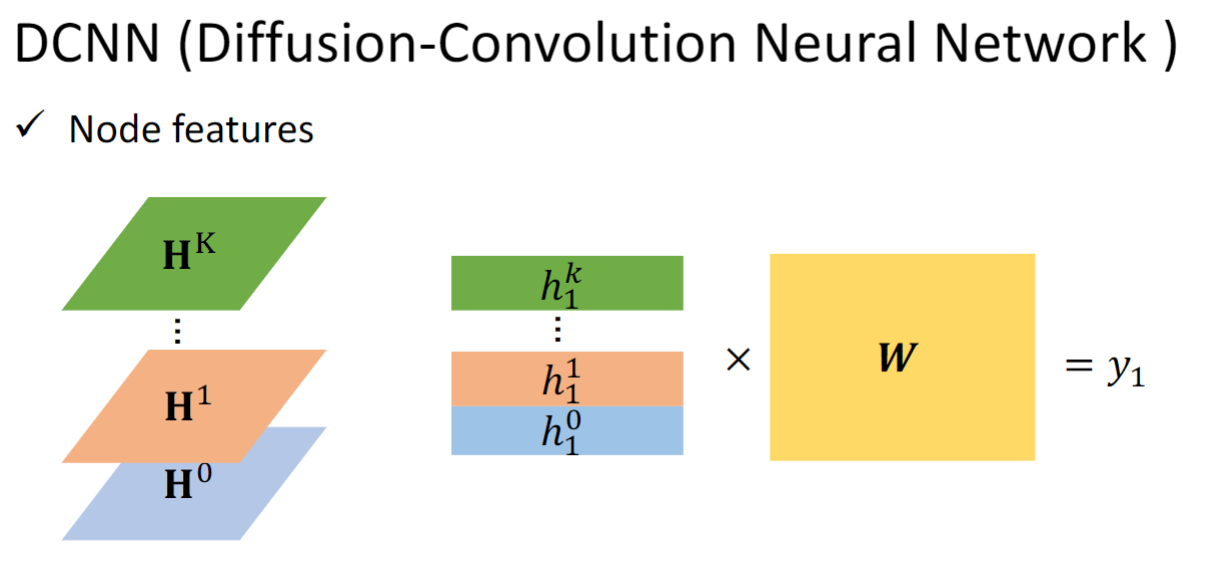
readout的做法如上图所示,无需多言.
MoNET (Mixture Model Networks)
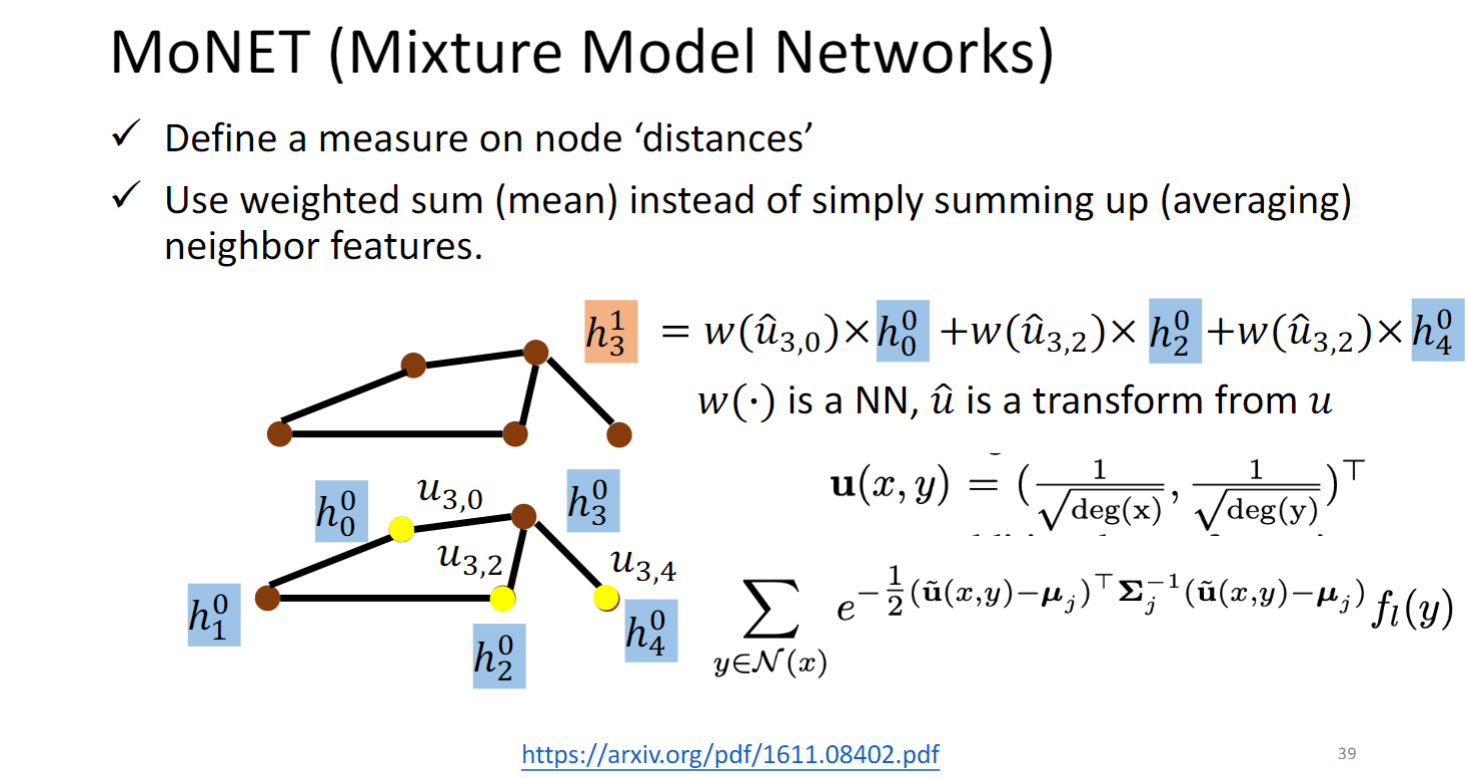
MoNET 对图中的边定义了距离权重,这篇文章中距离是由公式定义的,是可以直接计算的,也有的模型(GAT )是通过graph data学出的.
MoNET 将weighted sum neighbor features取代了NN4G和DCNN简单的相加求平均.
GAT (Graph Attention Networks)

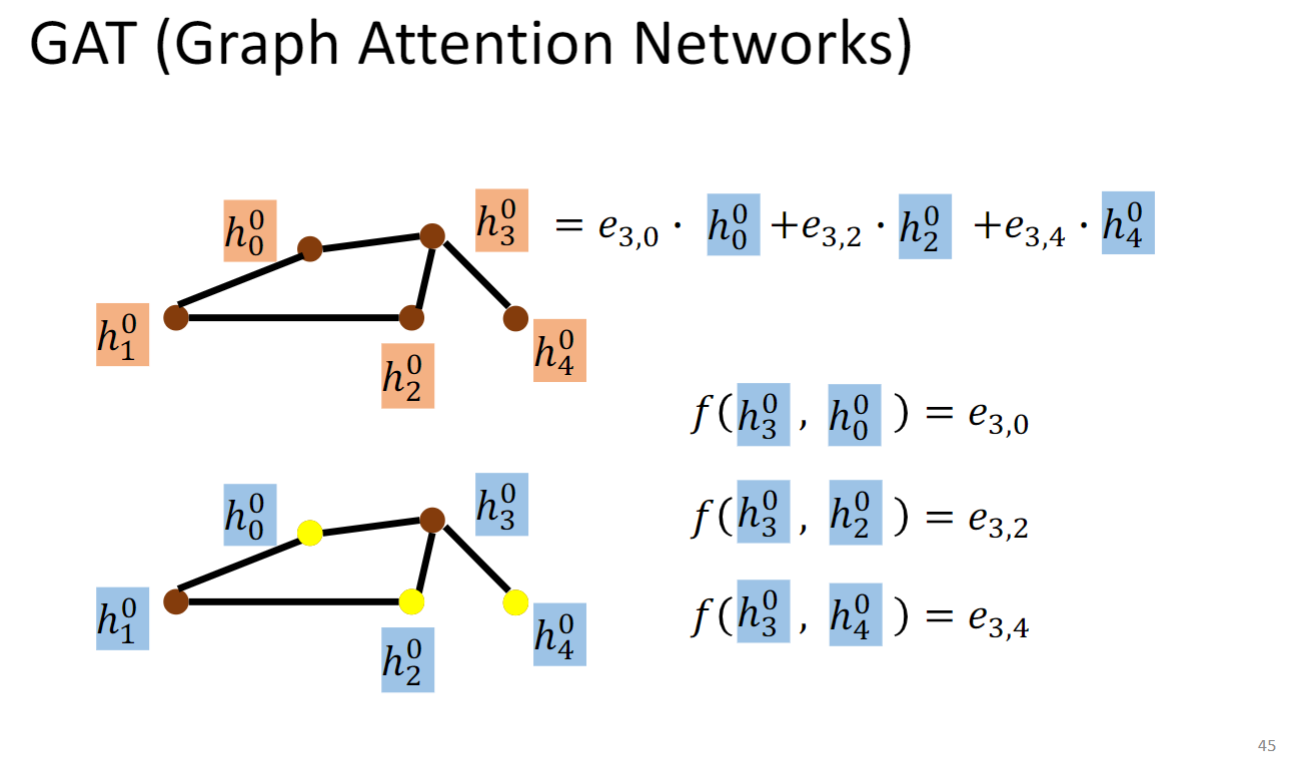
GAT计算节点在下一层上的hidden representation的时候,先算一个节点对它所有邻接节点的energy(即可变的weight) ,然后把这个energy作为权重乘上节点在当前层上的hidden representation,再求和(如上图所示),作为最终的在下一层的表示.
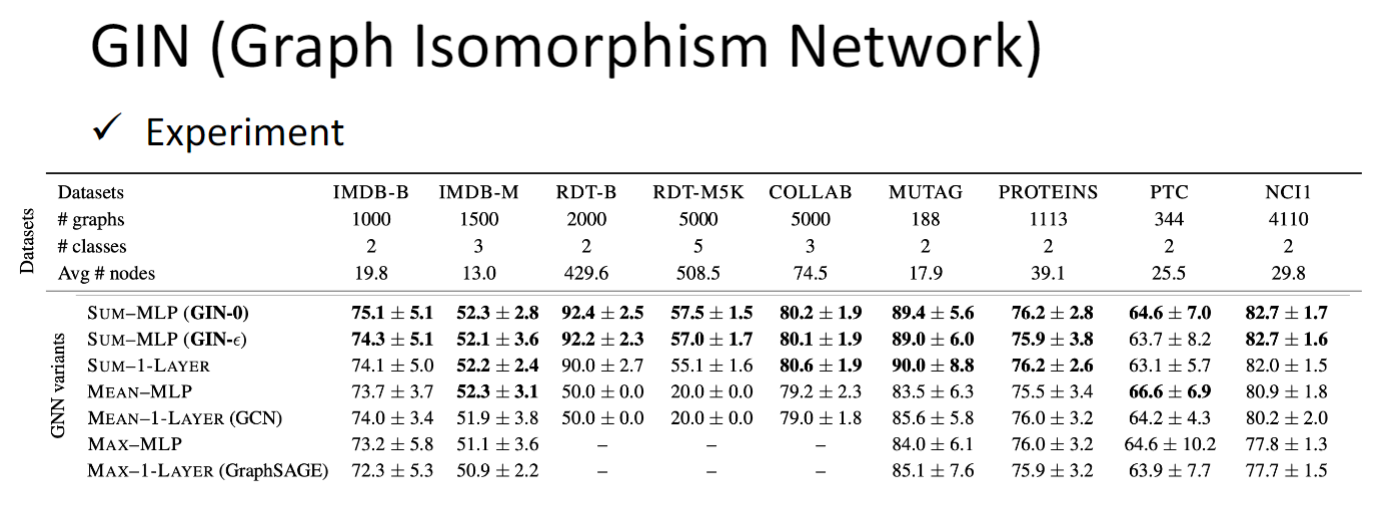
GIN (Graph Isomorphism Network)
前面的方法我们就直接用了,也没有问为什么它们会work,GIN这篇paper给出了一些证明,告诉你什么样的GNN model会work
- A GNN can be at most as powerful as WL isomorphic test
- Theoretical proofs were provided
结论:更新节点 representation 的时候最好使用下图中的公式所示的方式更新.
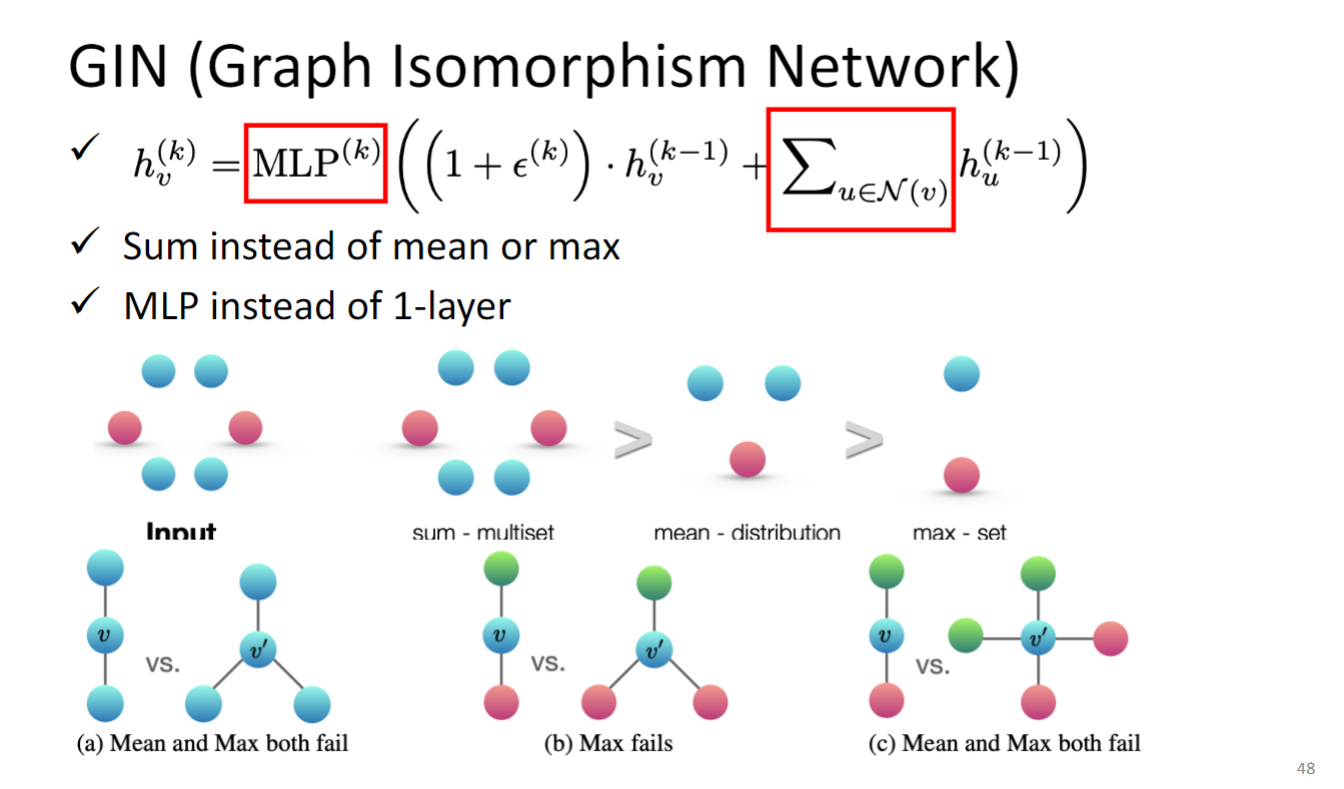
上图公式:
k是layer,v是node id,h update的方式应该要先将neighbor 全都加起来,而不能用max pooling也不能用mean pooling,然后加上某个constant 乘以 自己的feature,这个constant就是 $1 + \epsilon^{(k)} $ 这里的 是可以学出来的,但是paper中也说了这里设为0也没太大差别.
为什么不能用max pooling也不能用mean pooling,看上图下面一排:
a告诉我们,max or mean 无法区分a中的两个graph;
max无法分辨b中的两个graph;
max和mean也无法分辨c中的两个graph;
MLP是multi layer perceptron
Graph Signal Processing and Spectral-based GNN
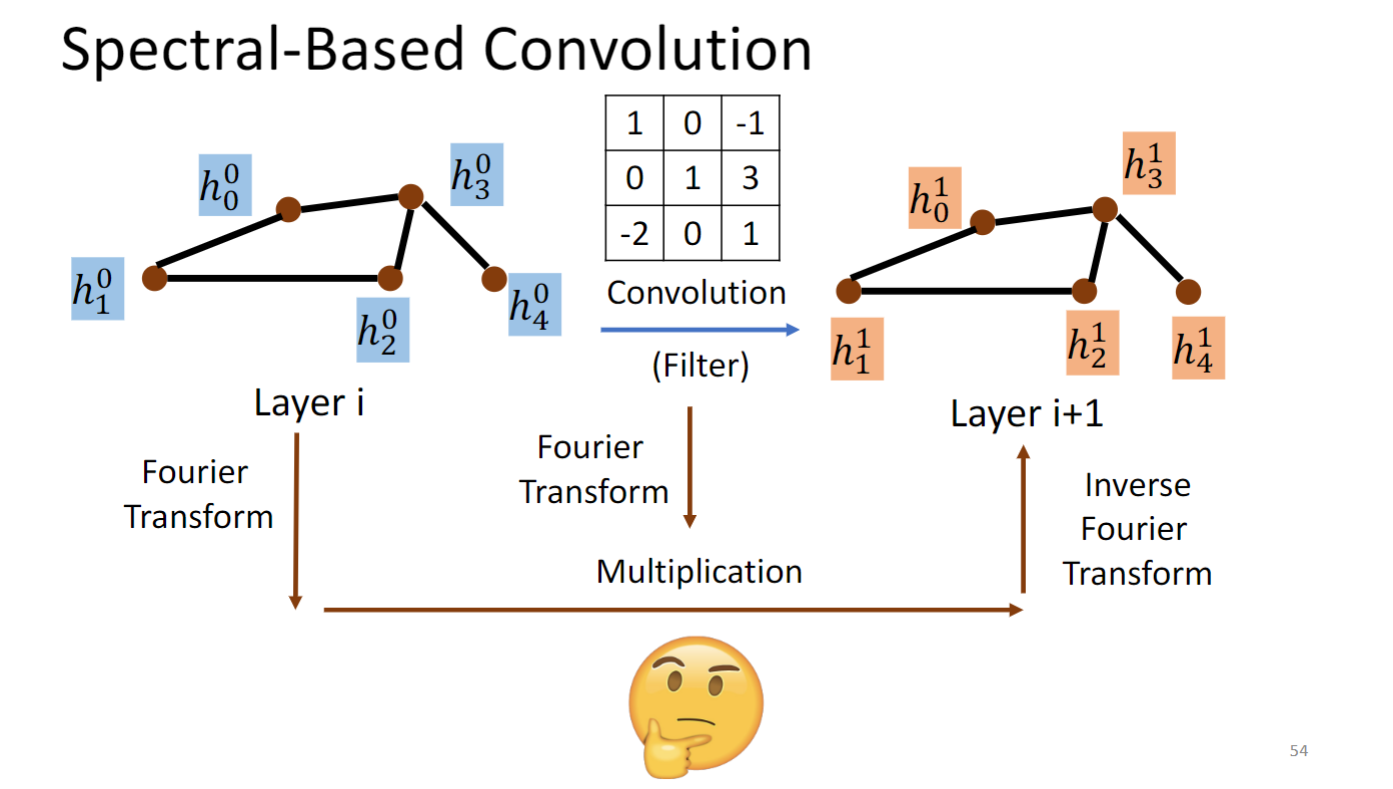
Spectral-based GNN 要做的事情就是将graph 和convolution kernel 都转换到傅里叶域中,在傅里叶域中做multiplication,再转换回去,就是得到下一个layer.
问题是这个傅里叶变换要怎么做呢,要回答这个问题要引入很多信号与系统的东西.
Warning of Math Signal And System
没学过信号与系统,听不懂,但不影响对整个GNN的理解(大概
如果想很好的理解下面讲的Spectral-based GNN的话,建议还是好好理解一下 Warning of Signal And System 这一部分.
ChebNet

主打特性是快,且localize
是拉普拉斯算子Laplacian的一个多项式函数,通过你选择让 是多项式函数的方式,你就可以让他是K-localized,因为根据上一节原理中讲的,如果你让g函数只到k次方,它就只能看到k-neighbor.
用Chebyshev 多项式解决时间复杂度太高的问题:
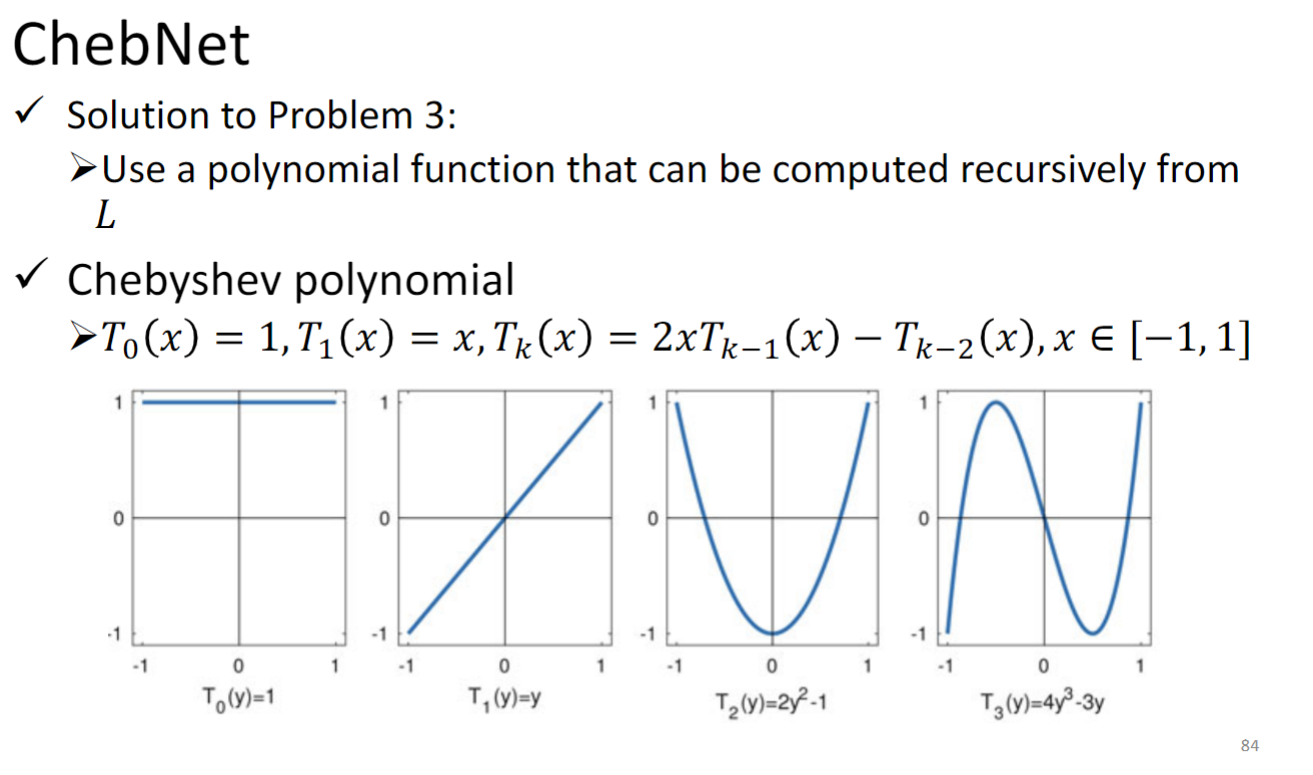
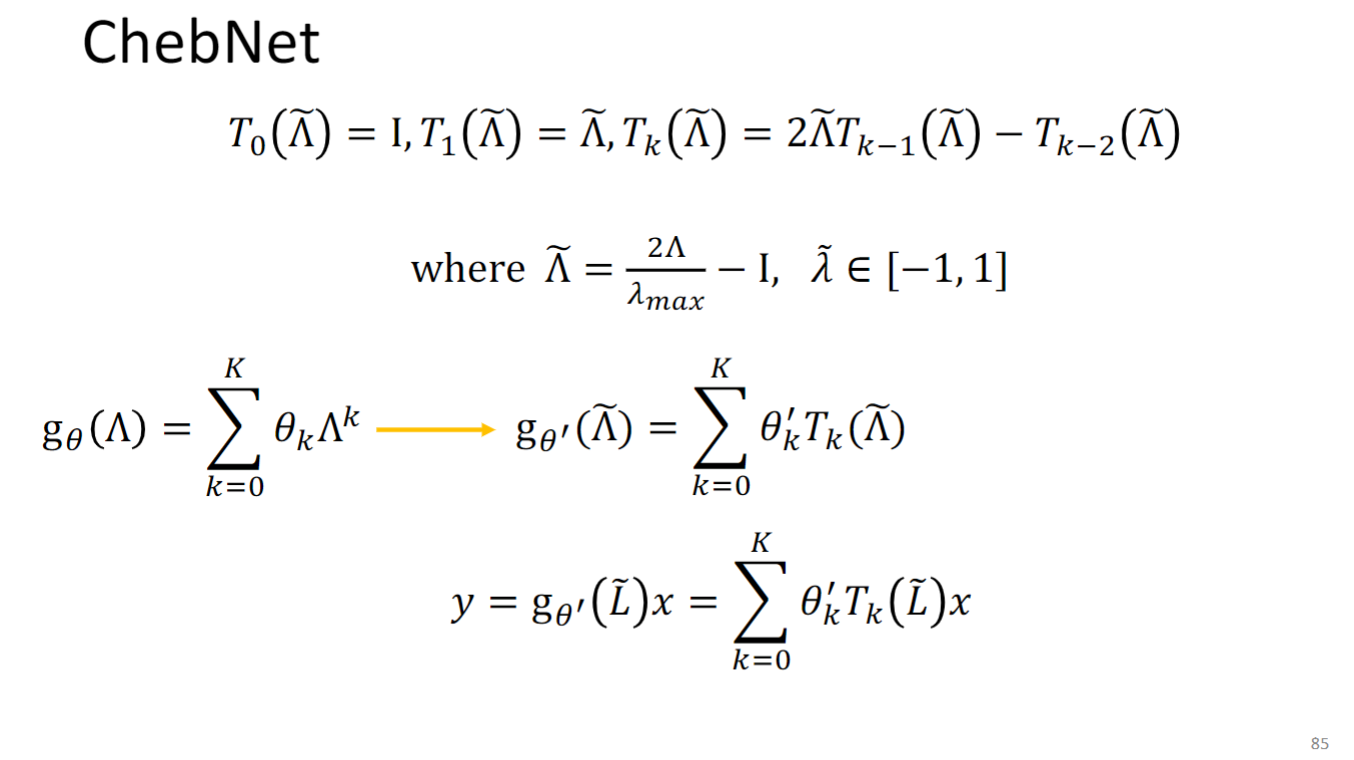
所以原本的 变为 ,怎么理解这个转换的作用,为什么要把一个多项式组合换成另一个多项式组合呢?你可以参考下面这个高中数学题:

你可以把 看成 把 看作后面的形式,这个转换使得 更容易计算了.
所以最后模型要学的东西就是 中的 .
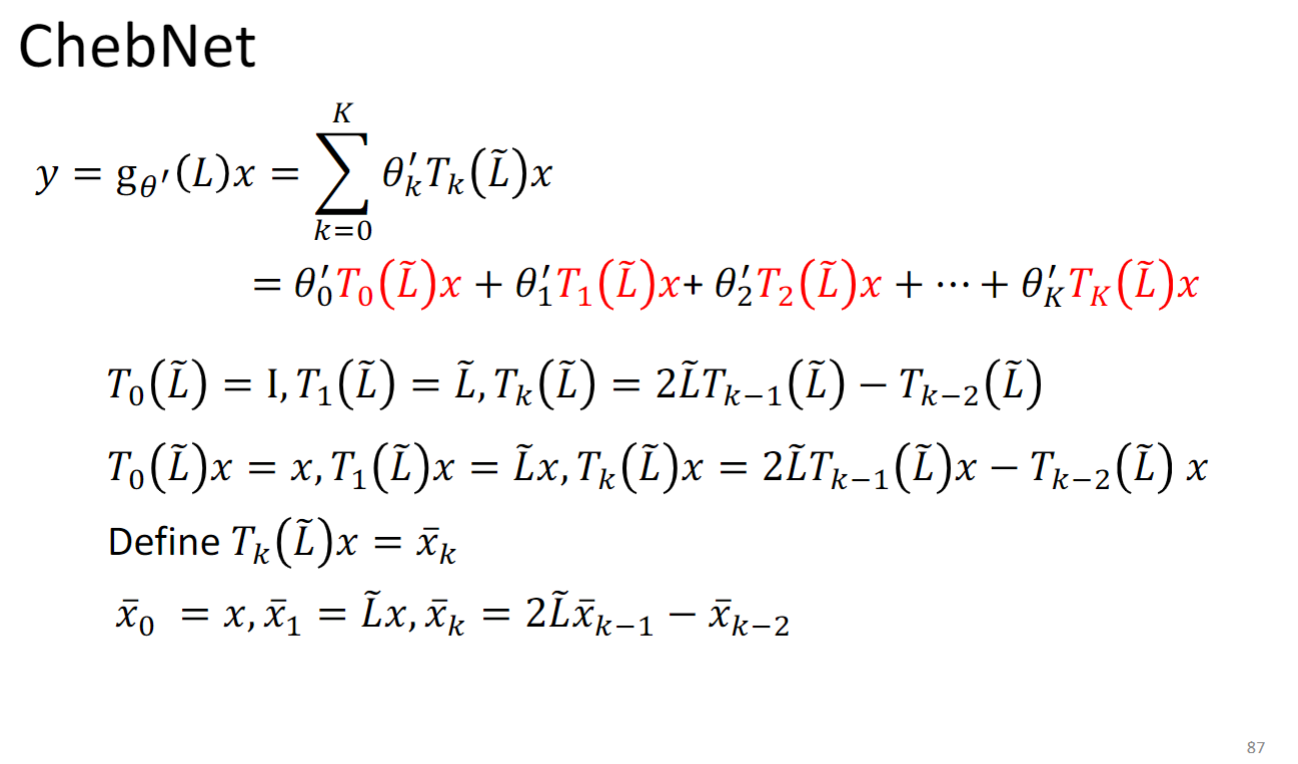
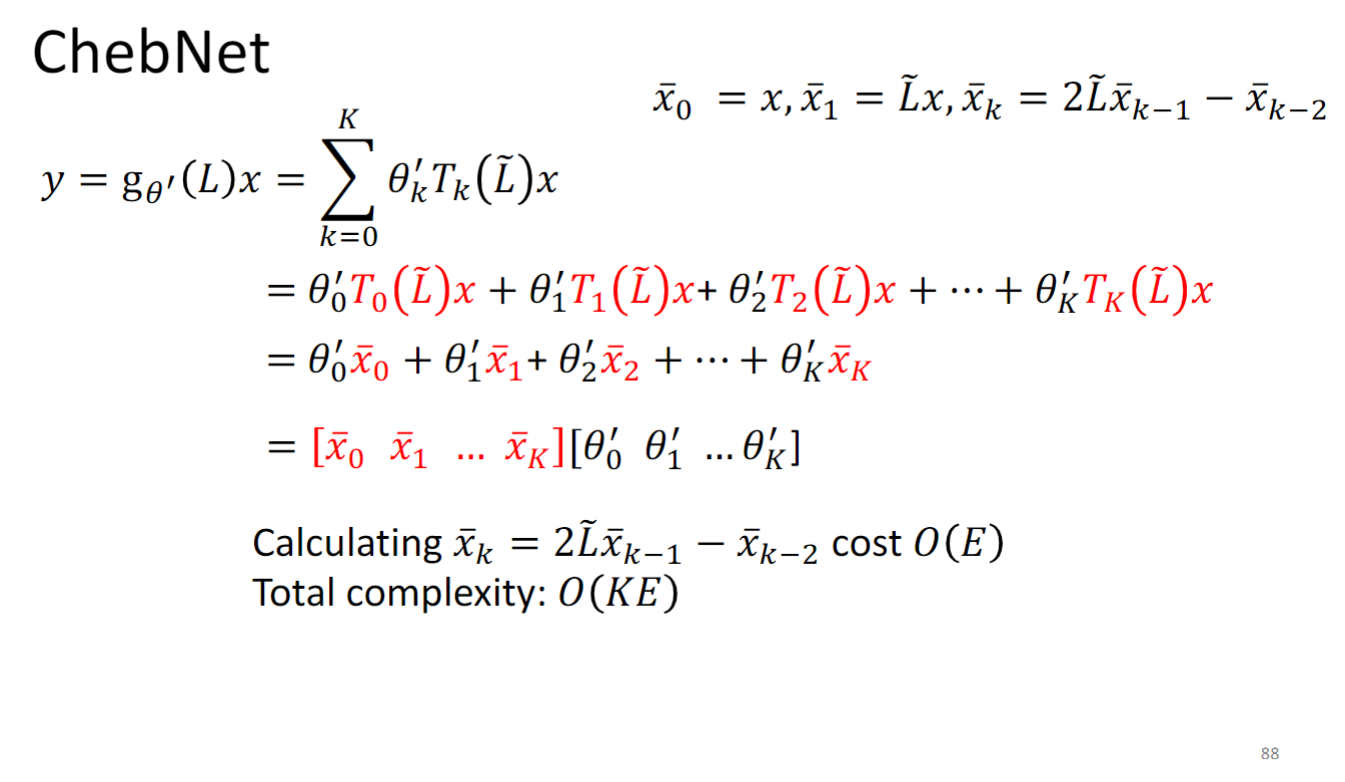
GCN
这是比较受喜欢的,被大家广泛使用的模型.

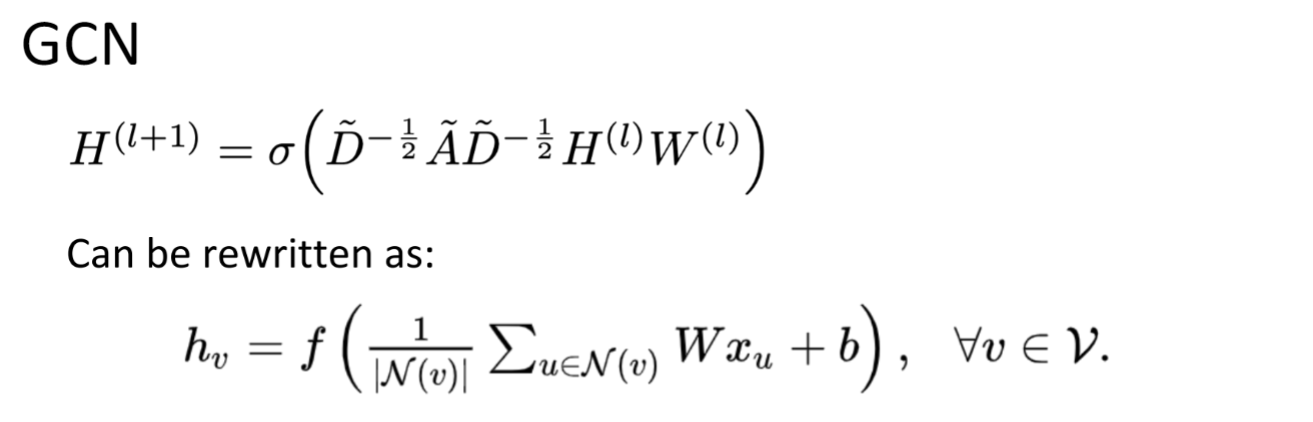
GCN对每个layer中的node 计算就是将所有neighbor包括他自己乘一个weight,再加起来,,再加上一个bias,再经过一个nonlinear activation,就结束.
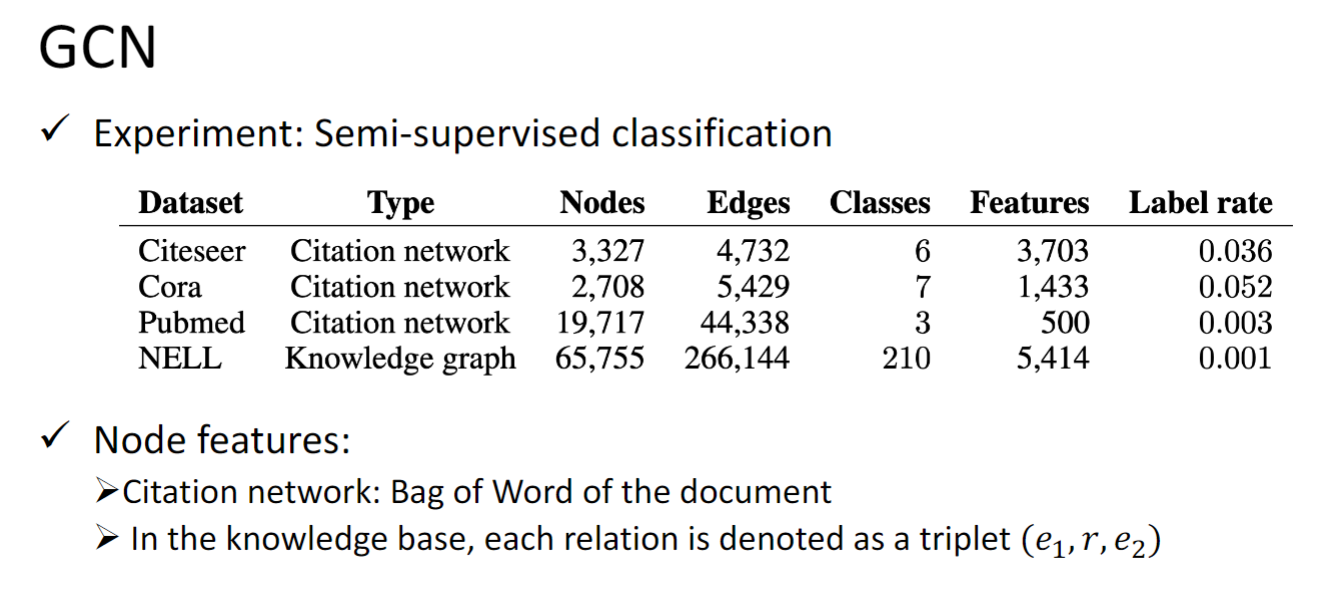
Graph Generation
- VAE-based model: Generate a whole graph in one step
- GAN-based model: Generate a whole graph in one step
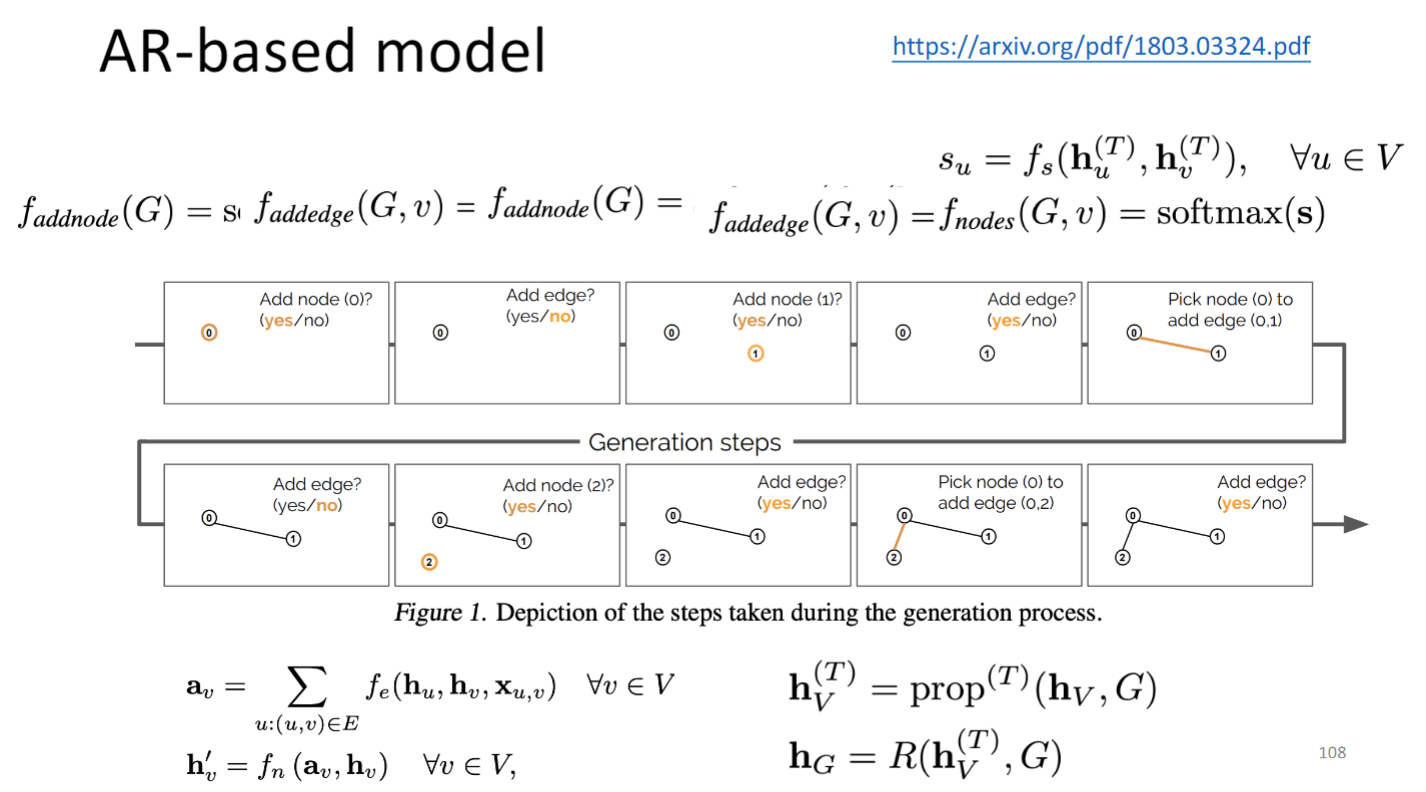
- Auto-regressive- based model: Generate a node or an edge in one step
VAE-based model
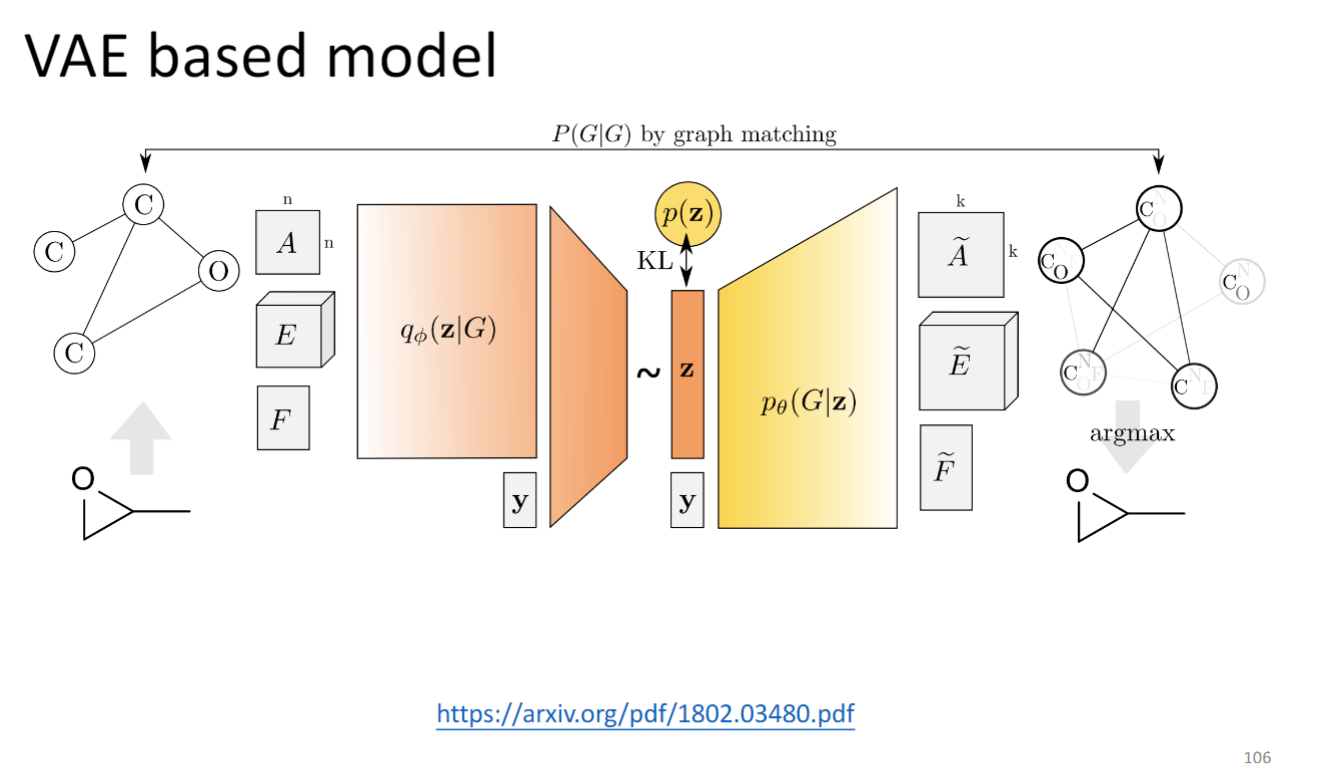
左边是encoder,右边是decoder,input是一个adjacency matrix,Edge Feature 和node Feature,生成一样是一个adjacency matrix,Edge Feature 和node Feature.
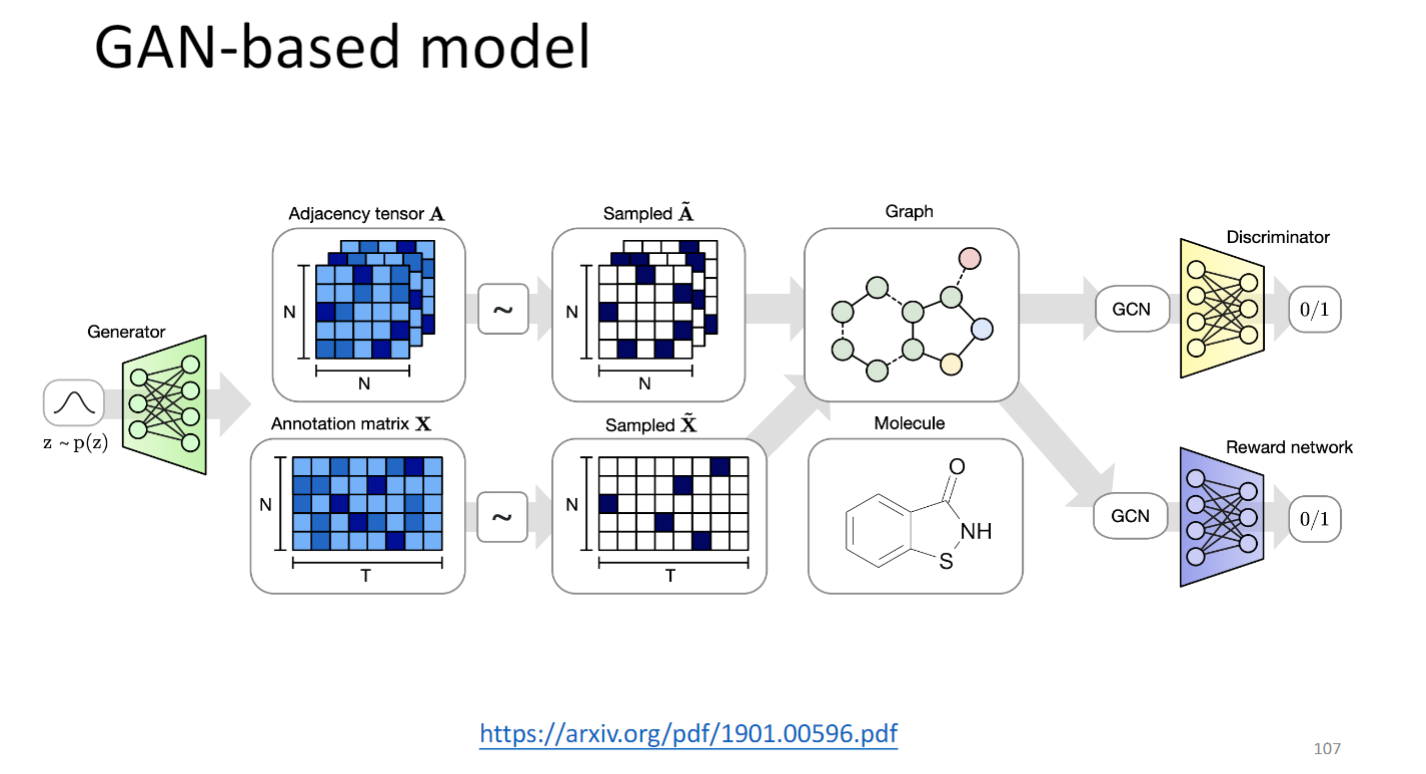
GAN的输入是adjacency matrix和feature matrix
Online Resources
PyTorch Geometric: https://github.com/rusty1s/pytorch_geometric
Deep Graph Library: http://dgl.ai/